服务调优

发表于 8月 13 2017 更新于 8月 25 2019 Valine：

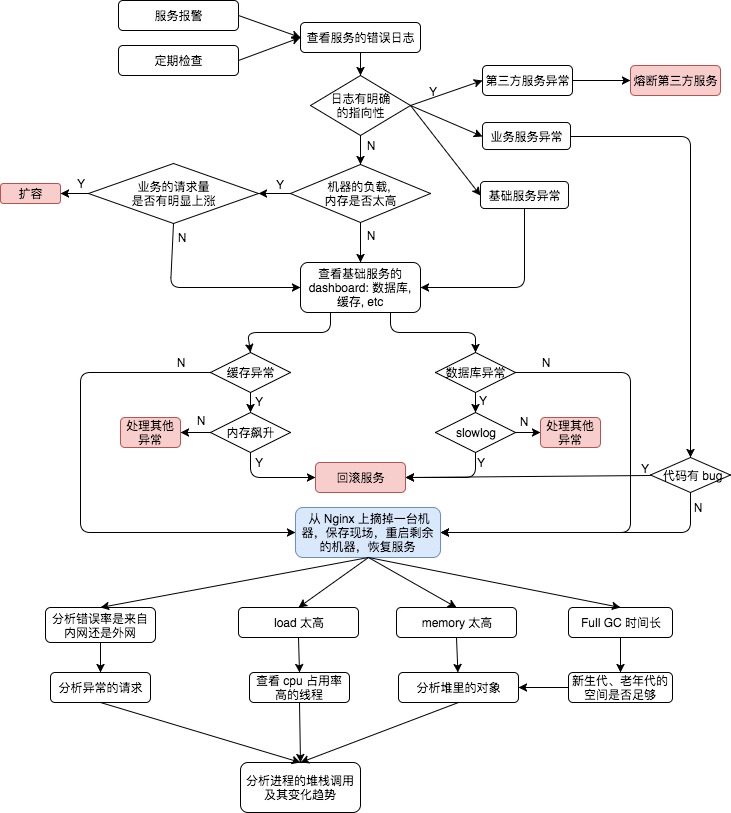
服务异常的处理流程

负载

查看机器 cpu 的负载

1	top -b -n 1 \|grep java\|awk '{print "VIRT:"$5,"RES:"$6,"cpu:"$9"%","mem:"$10"%"}'

查找 cpu 占用率高的线程

top -p 25603 -H
printf 0x%x 25842
jstack 25603 | grep 0x64f2

cat /proc/interrupts

（1）CPU
（2）Memory
（3）IO
（4）Network

可以从以下几个方面监控CPU的信息：
（1）中断；
（2）上下文切换；
（3）可运行队列；
（4）CPU 利用率。

内存

系统内存

free 命令
[root@server ~]# free

             total       used       free     shared    buffers     cached
Mem:       3266180    3250000      10000          0     201000    3002000
-/+ buffers/cache:      47000    3213000
Swap:      2048276      80160    1968116

这里的默认显示单位是kb。
各项指标解释

total:总计物理内存的大小。
used:已使用多大。
free:可用有多少。
Shared:多个进程共享的内存总额。
buffers: 磁盘缓存的大小。
cache:磁盘缓存的大小。
-/+ buffers/cached): used:已使用多大，free:可用有多少。
已用内存 = 系统used memory - buffers - cached
（47000 = 3250000-201000-3002000）
可用内存 = 系统free memory + buffers + cached
（3213000 = 10000+201000+3002000）

什么是buffer/cache？

buffer 指 Linux 内存的：Buffer cache，缓冲区缓
cache 指 Linux内存中的：Page cache，页面缓存

page cache
page cache 主要用来作为文件系统上的文件数据的缓存来用，尤其是针对当进程对文件有 read／write 操作的时候。如果你仔细想想的话，作为可以映射文件到内存的系统调用：mmap是不是很自然的也应该用到 page cache？在当前的系统实现里，page cache 也被作为其它文件类型的缓存设备来用，所以事实上 page cache 也负责了大部分的块设备文件的缓存工作。

buffer cache
buffer cache 主要用来在系统对块设备进行读写的时候，对块进行数据缓存的系统来使用。这意味着某些对块的操作会使用 buffer cache 进行缓存，比如我们在格式化文件系统的时候。一般情况下两个缓存系统是一起配合使用的，比如当我们对一个文件进行写操作的时候，page cache 的内容会被改变，而 buffer cache 则可以用来将 page 标记为不同的缓冲区，并记录是哪一个缓冲区被修改了。这样，内核在后续执行脏数据的回写（writeback）时，就不用将整个 page 写回，而只需要写回修改的部分即可。

在当前的内核中，page cache 是针对内存页的缓存，说白了就是，如果有内存是以page进行分配管理的，都可以使用page cache作为其缓存来管理使用。
当然，不是所有的内存都是以页（page）进行管理的，也有很多是针对块（block）进行管理的，这部分内存使用如果要用到 cache 功能，则都集中到buffer cache中来使用。（从这个角度出发，是不是buffer cache改名叫做block cache更好？）然而，也不是所有块（block）都有固定长度，系统上块的长度主要是根据所使用的块设备决定的，而页长度在X86上无论是32位还是64位都是4k。

系统如何回收cache？

Linux内核会在内存将要耗尽的时候，触发内存回收的工作，以便释放出内存给急需内存的进程使用。一般情况下，这个操作中主要的内存释放都来自于对buffer／cache的释放。尤其是被使用更多的cache空间。既然它主要用来做缓存，只是在内存够用的时候加快进程对文件的读写速度，那么在内存压力较大的情况下，当然有必要清空释放cache，作为free空间分给相关进程使用。所以一般情况下，我们认为buffer/cache空间可以被释放，这个理解是正确的。

但是这种清缓存的工作也并不是没有成本。理解cache是干什么的就可以明白清缓存必须保证cache中的数据跟对应文件中的数据一致，才能对cache进行释放。所以伴随着cache清除的行为的，一般都是系统IO飙高。因为内核要对比cache中的数据和对应硬盘文件上的数据是否一致，如果不一致需要写回，之后才能回收。

在系统中除了内存将被耗尽的时候可以清缓存以外，我们还可以人工触发缓存清除的操作。

进程内存

进程内存统计

/proc/[pid]/status
通过/proc//status可以查看进程的内存使用情况，包括虚拟内存大小（VmSize），物理内存大小（VmRSS），数据段大小（VmData），栈的大小（VmStk），代码段的大小（VmExe），共享库的代码段大小（VmLib）等等。

cat /proc/[pid]/status

Name: gedit /*进程的程序名*/
State: S (sleeping) /*进程的状态信息,具体参见http://blog.chinaunix.net/u2/73528/showart_1106510.html*/
Tgid: 9744 /*线程组号*/
Pid: 9744 /*进程pid*/
PPid: 7672 /*父进程的pid*/
TracerPid: 0 /*跟踪进程的pid*/
VmPeak: 60184 kB /*进程地址空间的大小*/
VmSize: 60180 kB /*进程虚拟地址空间的大小reserved_vm：进程在预留或特殊的内存间的物理页*/
VmLck: 0 kB /*进程已经锁住的物理内存的大小.锁住的物理内存不能交换到硬盘*/
VmHWM: 18020 kB /*文件内存映射和匿名内存映射的大小*/
VmRSS: 18020 kB /*应用程序正在使用的物理内存的大小，就是用ps命令的参数rss的值 (rss)*/
VmData: 12240 kB /*程序数据段的大小（所占虚拟内存的大小），存放初始化了的数据*/
VmStk: 84 kB /*进程在用户态的栈的大小*/
VmExe: 576 kB /*程序所拥有的可执行虚拟内存的大小,代码段,不包括任务使用的库 */
VmLib: 21072 kB /*被映像到任务的虚拟内存空间的库的大小*/
VmPTE: 56 kB /*该进程的所有页表的大小*/
Threads: 1 /*共享使用该信号描述符的任务的个数*/

JVM 内存分配

java内存组成介绍：堆(Heap)和非堆(Non-heap)内存

按照官方的说法：“Java 虚拟机具有一个堆，堆是运行时数据区域，所有类实例和数组的内存均从此处分配。堆是在 Java 虚拟机启动时创建的。”“在JVM中堆之外的内存称为非堆内存(Non-heap memory)”。可以看出JVM主要管理两种类型的内存：堆和非堆。简单来说堆就是Java代码可及的内存，是留给开发人员使用的；非堆就是JVM留给自己用的，所以方法区、JVM内部处理或优化所需的内存(如JIT编译后的代码缓存)、每个类结构(如运行时常数池、字段和方法数据)以及方法和构造方法的代码都在非堆内存中。

JVM本身需要的内存，包括其加载的第三方库以及这些库分配的内存
NIO的DirectBuffer是分配的native memory
内存映射文件，包括JVM加载的一些JAR和第三方库，以及程序内部用到的。上面 pmap 输出的内容里，有一些静态文件所占用的大小不在Java的heap里，因此作为一个Web服务器，赶紧把静态文件从这个Web服务器中人移开吧，放到nginx或者CDN里去吧。
JIT， JVM会将Class编译成native代码，这些内存也不会少，如果使用了Spring的AOP，CGLIB会生成更多的类，JIT的内存开销也会随之变大，而且Class本身JVM的GC会将其放到Perm Generation里去，很难被回收掉，面对这种情况，应该让JVM使用ConcurrentMarkSweep GC，并启用这个GC的相关参数允许将不使用的class从Perm Generation中移除，参数配置： -XX:+UseConcMarkSweepGC -X:+CMSPermGenSweepingEnabled -X:+CMSClassUnloadingEnabled，如果不需要移除而Perm Generation空间不够，可以加大一点： -X:PermSize=256M -X:MaxPermSize=512M
JNI，一些JNI接口调用的native库也会分配一些内存，如果遇到JNI库的内存泄露，可以使用valgrind等内存泄露工具来检测
线程栈，每个线程都会有自己的栈空间，如果线程一多，这个的开销就很明显了
jmap/jstack 采样，频繁的采样也会增加内存占用，如果你有服务器健康监控，记得这个频率别太高，否则健康监控变成致病监控了。

方法区

也称”永久代” 、“非堆”，它用于存储虚拟机加载的类信息、常量、静态变量、是各个线程共享的内存区域。默认最小值为16MB，最大值为64MB，可以通过-XX:PermSize 和 -XX:MaxPermSize 参数限制方法区的大小。

运行时常量池：是方法区的一部分，Class文件中除了有类的版本、字段、方法、接口等描述信息外，还有一项信息是常量池，用于存放编译器生成的各种符号引用，这部分内容将在类加载后放到方法区的运行时常量池中。

虚拟机栈

描述的是java 方法执行的内存模型：每个方法被执行的时候都会创建一个“栈帧”用于存储局部变量表(包括参数)、操作栈、方法出口等信息。每个方法被调用到执行完的过程，就对应着一个栈帧在虚拟机栈中从入栈到出栈的过程。声明周期与线程相同，是线程私有的。

局部变量表存放了编译器可知的各种基本数据类型(boolean、byte、char、short、int、float、long、double)、对象引用(引用指针，并非对象本身)，其中64位长度的long和double类型的数据会占用2个局部变量的空间，其余数据类型只占1个。局部变量表所需的内存空间在编译期间完成分配，当进入一个方法时，这个方法需要在栈帧中分配多大的局部变量是完全确定的，在运行期间栈帧不会改变局部变量表的大小空间。

本地方法栈

与虚拟机栈基本类似，区别在于虚拟机栈为虚拟机执行的java方法服务，而本地方法栈则是为Native方法服务。

堆

也叫做java 堆、GC堆是java虚拟机所管理的内存中最大的一块内存区域，也是被各个线程共享的内存区域，在JVM启动时创建。该内存区域存放了对象实例及数组(所有new的对象)。其大小通过-Xms(最小值)和-Xmx(最大值)参数设置，-Xms为JVM启动时申请的最小内存，默认为操作系统物理内存的1/64但小于1G，-Xmx为JVM可申请的最大内存，默认为物理内存的1/4但小于1G，默认当空余堆内存小于40%时，JVM会增大Heap到-Xmx指定的大小，可通过-XX:MinHeapFreeRation=来指定这个比列；当空余堆内存大于70%时，JVM会减小heap的大小到-Xms指定的大小，可通过XX:MaxHeapFreeRation=来指定这个比列，对于运行系统，为避免在运行时频繁调整Heap的大小，通常-Xms与-Xmx的值设成一样。

由于现在收集器都是采用分代收集算法，堆被划分为新生代和老年代。新生代主要存储新创建的对象和尚未进入老年代的对象。老年代存储经过多次新生代GC(Minor GC)任然存活的对象。

程序计数器

是最小的一块内存区域，它的作用是当前线程所执行的字节码的行号指示器，在虚拟机的模型里，字节码解释器工作时就是通过改变这个计数器的值来选取下一条需要执行的字节码指令，分支、循环、异常处理、线程恢复等基础功能都需要依赖计数器完成。

直接内存

直接内存并不是虚拟机内存的一部分，也不是Java虚拟机规范中定义的内存区域。jdk1.4中新加入的NIO，引入了通道与缓冲区的IO方式，它可以调用Native方法直接分配堆外内存，这个堆外内存就是本机内存，不会影响到堆内存的大小。

JVM 内存分析

查看 JVM 堆内存情况

jmap -heap [pid]

[root@server ~]$ jmap -heap 837
Attaching to process ID 837, please wait...
Debugger attached successfully.
Server compiler detected.
JVM version is 24.71-b01

using thread-local object allocation.
Parallel GC with 4 thread(s)//GC 方式

Heap Configuration: //堆内存初始化配置
   MinHeapFreeRatio = 0 //对应jvm启动参数-XX:MinHeapFreeRatio设置JVM堆最小空闲比率(default 40)
   MaxHeapFreeRatio = 100 //对应jvm启动参数 -XX:MaxHeapFreeRatio设置JVM堆最大空闲比率(default 70)
   MaxHeapSize      = 2082471936 (1986.0MB) //对应jvm启动参数-XX:MaxHeapSize=设置JVM堆的最大大小
   NewSize          = 1310720 (1.25MB)//对应jvm启动参数-XX:NewSize=设置JVM堆的‘新生代’的默认大小
   MaxNewSize       = 17592186044415 MB//对应jvm启动参数-XX:MaxNewSize=设置JVM堆的‘新生代’的最大大小
   OldSize          = 5439488 (5.1875MB)//对应jvm启动参数-XX:OldSize=<value>:设置JVM堆的‘老生代’的大小
   NewRatio         = 2 //对应jvm启动参数-XX:NewRatio=:‘新生代’和‘老生代’的大小比率
   SurvivorRatio    = 8 //对应jvm启动参数-XX:SurvivorRatio=设置年轻代中Eden区与Survivor区的大小比值 
   PermSize         = 21757952 (20.75MB)  //对应jvm启动参数-XX:PermSize=<value>:设置JVM堆的‘永生代’的初始大小
   MaxPermSize      = 85983232 (82.0MB)//对应jvm启动参数-XX:MaxPermSize=<value>:设置JVM堆的‘永生代’的最大大小
   G1HeapRegionSize = 0 (0.0MB)

Heap Usage://堆内存使用情况
PS Young Generation
Eden Space://Eden区内存分布
   capacity = 33030144 (31.5MB)//Eden区总容量
   used     = 1524040 (1.4534378051757812MB)  //Eden区已使用
   free     = 31506104 (30.04656219482422MB)  //Eden区剩余容量
   4.614088270399305% used //Eden区使用比率
From Space:  //其中一个Survivor区的内存分布
   capacity = 5242880 (5.0MB)
   used     = 0 (0.0MB)
   free     = 5242880 (5.0MB)
   0.0% used
To Space:  //另一个Survivor区的内存分布
   capacity = 5242880 (5.0MB)
   used     = 0 (0.0MB)
   free     = 5242880 (5.0MB)
   0.0% used
PS Old Generation //当前的Old区内存分布
   capacity = 86507520 (82.5MB)
   used     = 0 (0.0MB)
   free     = 86507520 (82.5MB)
   0.0% used
PS Perm Generation//当前的 “永生代” 内存分布
   capacity = 22020096 (21.0MB)
   used     = 2496528 (2.3808746337890625MB)
   free     = 19523568 (18.619125366210938MB)
   11.337498256138392% used

670 interned Strings occupying 43720 bytes.

关于这里的几个generation网上资料一大把就不细说了，这里算一下求和可以得知前者总共给Java环境分配了644M的内存，而ps输出的VSZ和RSS分别是7.4G和2.9G，这到底是怎么回事呢？
前面jmap输出的内容里，MaxHeapSize 是在命令行上配的，-Xmx4096m，这个java程序可以用到的最大堆内存。
VSZ是指已分配的线性空间大小，这个大小通常并不等于程序实际用到的内存大小，产生这个的可能性很多，比如内存映射，共享的动态库，或者向系统申请了更多的堆，都会扩展线性空间大小，要查看一个进程有哪些内存映射，可以使用 pmap 命令来查看：
pmap -x [pid]

[root@server ~]$ pmap -x 837
837:   java
Address           Kbytes     RSS   Dirty Mode   Mapping
0000000040000000      36       4       0 r-x--  java
0000000040108000       8       8       8 rwx--  java
00000000418c9000   13676   13676   13676 rwx--    [ anon ]
00000006fae00000   83968   83968   83968 rwx--    [ anon ]
0000000700000000  527168  451636  451636 rwx--    [ anon ]
00000007202d0000  127040       0       0 -----    [ anon ]
...
...
00007f55ee124000       4       4       0 r-xs-  az.png
00007fff017ff000       4       4       0 r-x--    [ anon ]
ffffffffff600000       4       0       0 r-x--    [ anon ]
----------------  ------  ------  ------
total kB         7796020 3037264 3023928

这里可以看到很多anon，这些表示这块内存是由mmap分配的。

RSZ是Resident Set Size，常驻内存大小，即进程实际占用的物理内存大小，在现在这个例子当中，RSZ和实际堆内存占用差了2.3G，这2.3G的内存组成分别为：

查看 JVM 堆各个分区的内存情况

jstat -gcutil [pid]

[root@server ~]$ jstat -gcutil 837 1000 20
  S0     S1     E      O      P     YGC     YGCT    FGC    FGCT     GCT   
  0.00  80.43  24.62  87.44  98.29   7101  119.652    40   19.719  139.371
  0.00  80.43  33.14  87.44  98.29   7101  119.652    40   19.719  139.371

分析 JVM 堆内存中的对象

查看存活的对象统计
jmap -histo:live [pid]

dump 内存
jmap -dump:format=b,file=heapDump [pid]

然后用jhat命令可以参看
jhat -port 5000 heapDump
在浏览器中访问：http://localhost:5000/ 查看详细信息

服务指标

响应时间(RT)

响应时间是指系统对请求作出响应的时间。直观上看，这个指标与人对软件性能的主观感受是非常一致的，因为它完整地记录了整个计算机系统处理请求的时间。由于一个系统通常会提供许多功能，而不同功能的处理逻辑也千差万别，因而不同功能的响应时间也不尽相同，甚至同一功能在不同输入数据的情况下响应时间也不相同。所以，在讨论一个系统的响应时间时，人们通常是指该系统所有功能的平均时间或者所有功能的最大响应时间。当然，往往也需要对每个或每组功能讨论其平均响应时间和最大响应时间。

对于单机的没有并发操作的应用系统而言，人们普遍认为响应时间是一个合理且准确的性能指标。需要指出的是，响应时间的绝对值并不能直接反映软件的性能的高低，软件性能的高低实际上取决于用户对该响应时间的接受程度。对于一个游戏软件来说，响应时间小于100毫秒应该是不错的，响应时间在1秒左右可能属于勉强可以接受，如果响应时间达到3秒就完全难以接受了。而对于编译系统来说，完整编译一个较大规模软件的源代码可能需要几十分钟甚至更长时间，但这些响应时间对于用户来说都是可以接受的。

吞吐量(Throughput)

吞吐量是指系统在单位时间内处理请求的数量。对于无并发的应用系统而言，吞吐量与响应时间成严格的反比关系，实际上此时吞吐量就是响应时间的倒数。前面已经说过，对于单用户的系统，响应时间（或者系统响应时间和应用延迟时间）可以很好地度量系统的性能，但对于并发系统，通常需要用吞吐量作为性能指标。

对于一个多用户的系统，如果只有一个用户使用时系统的平均响应时间是t，当有你n个用户使用时，每个用户看到的响应时间通常并不是n×t，而往往比n×t小很多（当然，在某些特殊情况下也可能比n×t大，甚至大很多）。这是因为处理每个请求需要用到很多资源，由于每个请求的处理过程中有许多不走难以并发执行，这导致在具体的一个时间点，所占资源往往并不多。也就是说在处理单个请求时，在每个时间点都可能有许多资源被闲置，当处理多个请求时，如果资源配置合理，每个用户看到的平均响应时间并不随用户数的增加而线性增加。实际上，不同系统的平均响应时间随用户数增加而增长的速度也不大相同，这也是采用吞吐量来度量并发系统的性能的主要原因。一般而言，吞吐量是一个比较通用的指标，两个具有不同用户数和用户使用模式的系统，如果其最大吞吐量基本一致，则可以判断两个系统的处理能力基本一致。

并发用户数

并发用户数是指系统可以同时承载的正常使用系统功能的用户的数量。与吞吐量相比，并发用户数是一个更直观但也更笼统的性能指标。实际上，并发用户数是一个非常不准确的指标，因为用户不同的使用模式会导致不同用户在单位时间发出不同数量的请求。一网站系统为例，假设用户只有注册后才能使用，但注册用户并不是每时每刻都在使用该网站，因此具体一个时刻只有部分注册用户同时在线，在线用户就在浏览网站时会花很多时间阅读网站上的信息，因而具体一个时刻只有部分在线用户同时向系统发出请求。这样，对于网站系统我们会有三个关于用户数的统计数字：注册用户数、在线用户数和同时发请求用户数。由于注册用户可能长时间不登陆网站，使用注册用户数作为性能指标会造成很大的误差。而在线用户数和同事发请求用户数都可以作为性能指标。相比而言，以在线用户作为性能指标更直观些，而以同时发请求用户数作为性能指标更准确些。

QPS每秒查询率(Query Per Second)

每秒查询率QPS是对一个特定的查询服务器在规定时间内所处理流量多少的衡量标准，在因特网上，作为域名系统服务器的机器的性能经常用每秒查询率来衡量。对应fetches/sec，即每秒的响应请求数，也即是最大吞吐能力。

从以上概念来看吞吐量和响应时间是衡量系统性能的重要指标，QPS虽然和吞吐量的计量单位不同，但应该是成正比的，任何一个指标都可以含量服务器的并行处理能力。当然Throughput更关心数据量，QPS更关心处理笔数。

CPU利用率

CPU Load Average < CPU个数核数 0.7

Context Switch Rate
就是Process（Thread）的切换，如果切换过多，会让CPU忙于切换，也会导致影响吞吐量。《高性能服务器架构》这篇文章的第2节就是说的是这个问题的。究竟多少算合适？google了一大圈，没有一个确切的解释。Context Switch大体上由两个部分组成：中断和进程(包括线程)切换，一次中断（Interrupt）会引起一次切换，进程（线程）的创建、激活之类的也会引起一次切换。CS的值也和TPS（Transaction Per Second）相关的，假设每次调用会引起N次CS，那么就可以得出

Context Switch Rate = Interrupt Rate + TPS* N

CSR减掉IR，就是进程/线程的切换，假如主进程收到请求交给线程处理，线程处理完毕归还给主进程，这里就是2次切换。也可以用CSR、IR、TPS的值代入公式中，得出每次事物导致的切换数。因此，要降低CSR，就必须在每个TPS引起的切换上下功夫，只有N这个值降下去，CSR就能降低，理想情况下N=0，但是无论如何如果N >= 4，则要好好检查检查。另外网上说的CSR<5000，我认为标准不该如此单一。

这三个指标在 LoadRunner 中可以监控到；另外，在 linux 中，也可以用 vmstat 查看r（Load Arerage），in（Interrupt）和cs（Context Switch）

工具

uptime

dmesg

top
查看进程活动状态以及一些系统状况

vmstat
查看系统状态、硬件和系统信息等

iostat
查看CPU 负载，硬盘状况

sar
综合工具，查看系统状况

mpstat
查看多处理器状况

netstat
查看网络状况

iptraf
实时网络状况监测

tcpdump
抓取网络数据包，详细分析

mpstat
查看多处理器状况

tcptrace
数据包分析工具

netperf
网络带宽工具

dstat
综合工具，综合了 vmstat, iostat, ifstat, netstat 等多个信息

Reference

>
http://tmq.qq.com/2016/07/it-is-necessary-to-know-the-background-performance-test/
https://www.ibm.com/developerworks/java/library/j-nativememory-linux/
http://www.oracle.com/technetwork/java/javase/index-137495.html
http://www.hollischuang.com/archives/303

使用 HBase 总结

发表于 5月 22 2016 更新于 8月 25 2019 Valine：

HBase 简介

HBase是Apache Hadoop的数据库，基于列存储、构建在HDFS上的分布式存储系统，能够对大型数据提供随机、实时的读写访问，是Google的BigTable的开源实现。HBase的目标是存储并处理大型的数据，仅用普通的硬件配置，就能够处理海量数据。

HBase 的优点

高可扩展性
HBase 是真正意义上的线性水平扩展。数据量累计到一定程度(可配置)，HBase系统会自动对数据进行水平切分，并分配不同的服务器来管理这些数据。这些数据可以被扩散到上千个普通服务器上。这样一方面可以由大量普通服务器组成大规模集群，来存放海量数据(从几个 TB 到几十 PB 的数据)。另一方面，当数据峰值接近系统设计容量时，可以简单通过增加服务器的方式来扩大容量。这个动态扩容过程无需停机，HBase系统可以照常运行并提供读写服务，完全实现动态无缝无宕机扩容。
高性能
HBase 的设计目的之一是支持高并发用户数的高速读写访问。这是通过两方面来实现的。首先数据行被水平切分并分布到多台服务器上，在大量用户访问时，访问请求也被分散到了不同的服务器上，虽然每个服务器的服务能力有限，但是数千台服务器汇总后可以提供极高性能的访问能力。其次，HBase 设计了高效的缓存机制，有效提高了访问的命中率，提高了访问性能。
高可用性
HBase 建立在 HDFS 之上。HDFS 提供了数据自动复制和容错的功能。HBase 的日志和数据都存放在 HDFS 上，即使在读写过程中当前服务器出现故障(硬盘、内存、网络等故障)，日志也不会丢失，数据都可以从日志中自动恢复。HBase 系统会自动分配其他服务器接管并恢复这些数据。因此一旦成功写入数据，这些数据就保证被持久化并被冗余复制，整个系统的高可用性得到保证。

数据模型

表
- 数据量：一张表可以有数十亿行，上百万列。
- 最大版本数：通常是3，如果对于更新比较频繁的应用完全可以设置为1，能够快速的淘汰无用数据，对于节省存储空间和提高查询速度有效果。不过这类需求在海量数据领域比较小众。
- 压缩算法：可以尝试一下最新出炉的snappy算法，相对lzo来说，压缩率接近，压缩效率稍高，解压效率高很多。
- inmemory：表在内存中存放，一直会被忽略的属性。如果完全将数据存放在内存中，那么hbase和现在流行的内存数据库memorycached和redis性能差距有多少，尚待实测。
- bloomfilter：根据应用来定，看需要精确到rowkey还是column。不过这里需要理解一下原理，bloomfilter的作用是对一个region下查找记录所在的hfile有用。即如果一个region下的hfile数量很多，bloomfilter的作用越明显。适合那种compaction赶不上flush速度的应用。
无模式
每行都有一个可排序的主键和任意多的列，列可以根据需要动态的增加，同一张表中不同的行可以有截然不同的列；
面向列
面向列（族）的存储和权限控制，列（族）独立检索；
稀疏
对于空（null）的列，并不占用存储空间，表可以设计的非常稀疏；
数据多版本
每个单元中的数据可以有多个版本，默认情况下版本号自动分配，是单元格插入时的时间戳；
数据类型单一
HBase中的数据都是字符串，没有类型。
存储单元 Cell
由{rowkey, colomnFamily:colomnQualifier, version} 确定的唯一单元，存储的数据是byte[]类型的。

HBase 的设计与实现

HBase 的架构

由上图可知，hbase包括Clinet、HMaster、HRegionServer、ZooKeeper组件
各组件功能介绍：

Client
Client主要通过ZooKeeper与Hbaser和HRegionServer通信，对于管理操作：client向master发起请求，对于数据读写操作：client向regionserver发起请求
ZooKeeper
zk负责存储_root_表的地址，也负责存储当前服务的master地址,regsion server也会将自身的信息注册到zk中，以便master能够感知region server的状态，zk也会协调active master，也就是可以提供一个选举master leader,也会协调各个region server的容灾流程
HMaster
master可以启动多个master，master主要负责table和region的管理工作，响应用户对表的CRUD操作，管理region server的负载均衡，调整region 的分布和分配，当region server停机后，负责对失效的regionn进行迁移操作
HRegionServer
region server主要负责响应用户的IO请求，并把IO请求转换为读写HDFS的操作

HBase 的架构详解

https://www.mapr.com/blog/in-depth-look-hbase-architecture#.VdMxvWSqqko

HBase, Mysql 的比较

Mysql 是关系型数据库，对于数据量不大(百万级别)，强依赖事务的业务，使用Mysql。
HBase 适用于对大数据进行随机、实时访问的场合，支持海量数据，扩展性好。
HBase 不适用的场景：

对分布式事务支持的不好
不支持多表的联合查询
对于复杂查询，需要扫描全表，且不支持索引

设计 HBase 表

RowKey 的设计

Rowkey唯一原则，必须在设计上保证其唯一性。但是还有几点需要注意的地方：

RowKey 长度的设计

Rowkey是一个二进制码流，可以是任意字符串，最大长度64KB，实际应用中一般为10~100bytes，存为byte[]字节数组。

定长
定长的好处是 RowKey 排序时是按字典序且不受不同长度的影响
短
不要超过16个字节。
- 数据的持久化文件 HFile 是按照 KeyValue 存储的，如果 Rowkey 过长比如100个字节，1000万列数据光 Rowkey 就要占用100*1000万=10亿个字节，将近1G数据，这会极大影响 HFile 的存储效率；
- MemStore 将缓存部分数据到内存，如果 Rowkey 字段过长内存的有效利用率会降低，系统将无法缓存更多的数据，这会降低检索效率。
16个字节
目前操作系统是都是64位系统，内存8字节对齐。控制在16个字节，8字节的整数倍利用操作系统的最佳特性。

RowKey 含义的设计

RowKey 虽然是越短越好，但也需要考虑 RowKey 的含义。由于 HBase 是按字典序存储，所以 RowKey 设计的合理可以提高查询效率(因为这会提高 RegionServer 的缓存命中率)，并且有意义的 RowKey 也便于在 scan 表的时候确定 startRow 和 stopRow。

RowKey 包含时间
不要将时间放在二进制码的前面，建议将 RowKey 的高位作为散列字段（或者本身就已经是散列的其他id，例如userId），低位放时间字段。否则最新的数据都集中放在某个 RegionServer，而访问量又都集中在最新的数据上，将会导致 Hotspotting 现象，降低了访问速度，同时也增加了 RegionServer Crash 的概率。
但考虑到是按字典序存储，如果想让最新的数据在最前面，可以使用 Long.MAX_VALUE – timestamp 作为 RowKey 的一部分。
RowKey 包含多个含义时
各个含义用某种分隔符分开，比如包含用户，类型，时间三种含义的 RowKey, 可以设计为 userId#type#timestamp，这样如果需要查找某个用户某段时间的数据，scan 时只需要根据 userId 设置 startRow 和 stopRow 即可。

RowKey 性能的设计

RowKey 是按照字典序存储，利用这个排序特点，将经常一起读取或者最近可能被访问到的数据存储到一块可以提高查询效率。

Hotspotting
It is always advisable not to use sequential row keys, even though you get better scan results. More info here.
Salting Row Key. To prevent hot spotting on writes, the row key may be “salted” by inserting a leading byte into the row key which is a mod over N buckets of the hash of the entire row key. This ensures even distribution of writes when the row key is a monotonically increasing value (often a timestamp representing the current time).
Length of row key
For each cell, rowkey details, column family, and qualifier details are stored. So it is always advisable to keep them as shot as possible, mainly because the same information is repeated on large scale.
So whats next
salt usage and its prefixing will help to distribute the rows among region servers.This can help you.

ColumnFamily 的设计

ColumnFamily 的长度

The column family and column qualifier names are repeated for each row. Therefore, keep the names as short as possible to reduce the amount of data that HBase stores and reads. For example, use f:q instead of mycolumnfamily:mycolumnqualifier.

ColumnFamily 的数量

On the number of column families
HBase currently does not do well with anything above two or three column families so keep the number of column families in your schema low. Currently, flushing and compactions are done on a per Region basis so if one column family is carrying the bulk of the data bringing on flushes, the adjacent families will also be flushed though the amount of data they carry is small. When many column families the flushing and compaction interaction can make for a bunch of needless i/o loading (To be addressed by changing flushing and compaction to work on a per column family basis). For more information on compactions, see compaction. (具体的细节见第2节)

Try to make do with one column family if you can in your schemas. Only introduce a second and third column family in the case where data access is usually column scoped; i.e. you query one column family or the other but usually not both at the one time.

Where multiple ColumnFamilies exist in a single table, be aware of the cardinality (i.e., number of rows). If ColumnFamilyA has 1 million rows and ColumnFamilyB has 1 billion rows, ColumnFamilyA’s data will likely be spread across many, many regions (and RegionServers). This makes mass scans for ColumnFamilyA less efficient.

建议HBASE列族的数量设置的越少越好。由于HBASE的FLUSHING和压缩是基于REGION的当一个列族所存储的数据达到FLUSHING阀值时，该表的所有列族将同时进行FLASHING操作，这将带来不必要的I/O开销。同时还要考虑到同一个表中不同列族所存储的记录数量的差别，即列族的势。当列族数量差别过大将会使包含记录数量较少的列族的数据分散在多个Region之上，而Region可能是分布是不同的RegionServer上。这样当进行查询等操作系统的效率会受到一定影响。

Column 的设计

Column 的长度

Column 的数量

Column mapping: one to many
You can map a single HBase entity (row key or a column) to multiple SQL columns. This kind of mapping is called one to many. HBase stores a lot of information for each value. If you stored each SQL column individually, the required storage space would be very large. For the best performance, put columns that are queried together into a single dense HBase column to help reduce the data that is fetched from HBase. A dense column is a single HBase column that maps to multiple SQL columns.

For example, if table T1 has nine columns with 1.5 million rows. and you use a one-to-one mapping, this table requires 522 MB of storage. However, if table T1 uses a one-to-many mapping, the table requires only 276 MB of storage.

读 HBase 的性能

HBase Pool

Use pool of workers to parallel requests. You may find useful HTablePool class for managing connections in workers.

批量读

通过调用 HTable.get(Get) 方法可以根据一个指定的 RowKey 获取一行记录，同样 HBase 提供了另一个方法：通过调用 HTable.get(List) 方法可以根据一个指定的 RowKey 列表，批量获取多行记录，这样做的好处是批量执行，只需要一次网络I/O开销，这对于对数据实时性要求高而且网络传输RTT高的情景下可能带来明显的性能提升。

Scan

Scanner Caching
hbase.client.scanner.caching配置项可以设置HBase scanner一次从服务端抓取的数据条数，默认情况下一次一条。通过将其设置成一个合理的值，可以减少scan过程中next()的时间开销，代价是 scanner需要通过客户端的内存来维持这些被cache的行记录。
Scan AttributeSelection
scan时指定需要的Column Family，可以减少网络传输数据量，否则默认scan操作会返回整行所有Column Family的数据。
Close ResultScanner
通过scan取完数据后，记得要关闭ResultScanner，否则RegionServer可能会出现问题（对应的Server资源无法释放）。

PrefixFilter

PefixFilter Vs Scan

HBase filters - even row filters - are really slow, since in most cases these do a complete table scan, and then filter on those results.
Row key range scans however, are indeed much faster - they do the equivalent of a filtered table scan. This is because the row keys are stored in sorted order (this is one of the basic guarantees of HBase, which is a BigTable-like solution), so the range scans on row keys are very fast.

Convert PrefixFilter to Scan

PrefixFilter: abc
Scan ‘mytable’, {STARTROW => ‘abc’, ENDROW => ‘abd’}

如何解决事务

transactions over hbase
The way HBase works is that locks are held in the regionserver (not in the client) when the Puts are applied to make sure that rows are written in an atomic block but it does not provide snapshot isolation (you need to use something like omid if you want that).

Since HBase does not guarantee any consistency between regions (and each region is hosted at exactly one RegionServer) all MVCC data structures only need to be kept in memory on every region server.

I would probably not use HBase for a use case like this. but if you must you can lock the row, read, update if needed - read more about lock and some of its problems here ngdata.com/hbase-row-locks . Again, I’d try to rethink the scenario for instance, HBase support multiple version so you can update anyway and sort things later (e.g. in a coprocessor that runs after update)
RowLock and associated operations are deprecated in 0.94 and removed in 0.96.issues.apache.org/jira/browse/HBASE-7315 – Matt Ball

hbase checkAndPut
hbase checkandput performance
When you use checkAndPut() you do one RPC-call per request. So, you can’t achieve performance more then 1 / rtt requests per second (rtt is Round Trip Time). If you have rtt 1ms between your client and region server, your theoretical maximum is 1000 rps. When using batch operations like put(List) you need a lot less RPC-calls causing performance increase.

Reference

http://blog.linezing.com/2012/03/hbase-performance-optimization/
https://www.ibm.com/support/knowledgecenter/SSPT3X_2.1.2/com.ibm.swg.im.infosphere.biginsights.analyze.doc/doc/bigsql_designhints.html
http://blog.kissdata.com/2014/07/30/hbase-scheme-tips.html
http://blog.chedushi.com/archives/9720
https://www.mapr.com/blog/in-depth-look-hbase-architecture#.VdMxvWSqqko
https://cloud.google.com/bigtable/docs/schema-design
http://www.slideshare.net/alexbaranau/transactions-over-hbase
https://hbase.apache.org/acid-semantics.html

https详解

发表于 4月 17 2016 更新于 8月 25 2019 Valine：

什么是https

也称作HTTP over TLS

什么是SSL/TLS

1994年，NetScape公司设计了SSL协议（Secure Sockets Layer）的1.0版，但是未发布。
1995年，NetScape公司发布SSL 2.0版，很快发现有严重漏洞。
1996年，SSL 3.0版问世，得到大规模应用。
1999年，互联网标准化组织ISOC接替NetScape公司，发布了SSL的升级版TLS 1.0版。
2006年和2008年，TLS进行了两次升级，分别为TLS 1.1版和TLS 1.2版。最新的变动是2011年TLS 1.2的修订版。
TLS 1.0通常被标示为SSL 3.1，TLS 1.1为SSL 3.2，TLS 1.2为SSL 3.3。

为什么要有https

在说HTTPS之前先说说什么是HTTP，HTTP就是我们平时浏览网页时候使用的一种协议。HTTP协议传输的数据都是未加密的，也就是明文的，因此使用HTTP协议传输隐私信息非常不安全。为了保证这些隐私数据能加密传输，于是网景公司设计了SSL（Secure Sockets Layer）协议用于对HTTP协议传输的数据进行加密，从而就诞生了HTTPS。

https保证安全的原理

Client端和Server端如果用非对称加密的算法进行通信肯定是绝对安全的，因为私钥和密钥没有第三方知道。但是这样的问题是性能低下。但是如果用对称加密，很容易泄露密钥，安全性得不到保证。那么https是如何做的呢？
大概原理就是使用非对称加密来交换一个密钥来进行对称加密。这个过程被称为SSL/TSL的四次握手，具体过程如下：

Client端向Server端的443端口发出请求，带上随机数client_random和支持的加密方式列表
Server端返回随机数server_random ，选择的加密方式和服务器证书链
Client端验证这个证书是否合法，如果非法则提示用户是否“继续接受这个不可信的网站”，如果合法则使用证书中的公钥加密premaster secret发送给服务端
Server端使用私钥解密premaster secret，然后通过client_random，server_random 和premaster secret 生成master secret，用于对称加密后续通信内容。
Sever端用master secret加密最终需要返回的网站内容
Client端也用相同的方式生成这个master secret解密收到的消息

master_secret = PRF(pre_master_secret, “master secret”, ClientHello.random + ServerHello.random)[0..47];

随机数为什么要三个？
这是由于SSL/TLS设计，就假设服务器不相信所有的客户端都能够提供完全随机数，假如某个客户端提供的随机数不随机的话，就大大增加了“对话密钥”被破解的风险，所以由三组随机数组成最后的随机数，保证了随机数的随机性，以此来保证每次生成的“对话密钥”安全性。

那么问题来了

证书的安全性，Client端是如何验证证书合法性的，这个证书第三方无论如何都伪造不了吗？
对称加密密钥的安全性，生成的master secret密钥第三方为什么拿不到？

要解答这两个问题，首先得弄清楚什么是证书。

为什么证书是安全的？

什么是证书

数字证书就是互联网通讯中标志通讯各方身份信息的一串数字，提供了一种在Internet上验证通信实体身份的方式，数字证书不是数字身份证，而是身份认证机构盖在数字身份证上的一个章或印（或者说加在数字身份证上的一个签名）。它是由权威机构——CA机构，又称为证书授权（Certificate Authority）中心发行的，人们可以在网上用它来识别对方的身份。
数字证书的格式普遍采用的是X.509V3国际标准，一个标准的X.509数字证书包含以下一些内容：

证书的版本信息；
证书的序列号，每个证书都有一个唯一的证书序列号；
证书所使用的签名算法；
证书的发行机构名称，命名规则一般采用X.500格式；
证书的有效期，通用的证书一般采用UTC时间格式，它的计时范围为1950-2049；
证书所有人的名称，命名规则一般采用X.500格式；
证书所有人的公开密钥；
证书发行者对证书的签名。

证书里的公钥的作用？
证书里的签名的作用？
数字证书的签发机构CA，在接收到申请者的资料后进行核对并确定信息的真实有效，然后就会制作一份符合X.509标准的文件。证书中的证书内容包含的持有者信息和公钥等都是由申请者提供的，而数字签名则是CA机构对证书内容进行hash加密后得到的，而这个数字签名就是我们验证证书是否是有可信CA签发的数据。

证书的产生

证书的类型

实际上，我们使用的证书分很多种类型，SSL证书只是其中的一种。证书的格式是由X.509标准定义。SSL证书负责传输公钥，是一种PKI（Public Key Infrastructure，公钥基础结构）证书。
我们常见的证书根据用途不同大致有以下几种：
1、SSL证书，用于加密HTTP协议，也就是HTTPS。
2、代码签名证书，用于签名二进制文件，比如Windows内核驱动，Firefox插件，Java代码签名等等。
3、客户端证书，用于加密邮件。
4、双因素证书，网银专业版使用的USB Key里面用的就是这种类型的证书。
这些证书都是由受认证的证书颁发机构——我们称之为CA（Certificate Authority）机构来颁发，针对企业与个人的不同，可申请的证书的类型也不同，价格也不同。CA机构颁发的证书都是受信任的证书，对于SSL证书来说，如果访问的网站与证书绑定的网站一致就可以通过浏览器的验证而不会提示错误。

证书的安全问题

如果让证书安全，那么就需要让客户端拿到的证书是真正想要的证书，即不能让证书被冒充或者被篡改。
那么如何保证这一点呢？

如果证书自己有一个id
证书的这个id无法被伪造
客户端知道自己想要的证书id是多少

如果做到了这三点就能保证证书的安全性了。上面说提到的id就是证书的数字签名。那么什么是数字签名？

数字签名（digital signature）

数字签名是证书的防伪标签，是将待签名内容通过哈希和私钥加密处理后生成的。目前使用最广泛的 SHA-RSA 数字签名的制作和验证过程如下：

数字签名的签发。首先是使用哈希函数对待签名内容进行安全哈希，生成数字摘要，然后使用CA自己的私钥对数字摘要进行加密。
数字签名的校验。使用CA的公钥解密签名，然后使用相同的签名函数对待签名证书内容进行签名并和服务端数字签名里的签名内容进行比较，如果相同就认为校验成功。

签发：待签名内容 -> 哈希 -> 数字摘要 -> CA私钥加密 -> 数字签名
校验：

数字签名 -> CA公钥解密 -> 数字摘要1
待签名内容 -> 哈希 -> 数字摘要2
比较「数字摘要1」和「数字摘要2」是否相等

这里有几点需要说明：

数字签名签发和校验使用的密钥对是 CA 自己的公私密钥，跟证书申请者提交的公钥没有关系。
数字签名的签发过程跟公钥加密的过程刚好相反，即是用私钥加密，公钥解密。
现在大的 CA 都会有证书链，证书链的好处一是安全，保持根 CA 的私钥离线使用。第二个好处是方便部署和撤销，即如果证书出现问题，只需要撤销相应级别的证书，根证书依然安全。
根 CA 证书都是自签名，即用自己的公钥和私钥完成了签名的制作和验证。而证书链上的证书签名都是使用上一级证书的密钥对完成签名和验证的。

那么问题又来了。
CA的私钥和公钥是安全的吗？可以被冒充吗？

CA的安全性

从根CA开始到直接给客户发放证书的各层次CA，都有其自身的密钥对。CA中心的密钥对一般由硬件加密服务器在机器内直接产生，并存储于加密硬件内，或以一定的加密形式存放于密钥数据库内。加密备份于IC卡或其他存储介质中，并以高等级的物理安全措施保护起来。密钥的销毁要以安全的密钥冲写标准，彻底清除原有的密钥痕迹。需要强调的是，根CA密钥的安全性至关重要，它的泄露意味着整个公钥信任体系的崩溃，所以CA的密钥保护必须按照最高安全级的保护方式来进行设置和管理。

CA的私钥是自己靠上述方法保管的，不对外公开。
CA的公钥是厂商跟浏览器和操作系统合作，把公钥默认装到浏览器或者操作系统环境里。比如firefox 就自己维护了一个可信任的 CA 列表，而chrome 和 IE 使用的是操作系统的 CA 列表。

证书验证失败的原因

1、SSL证书不是由受信任的CA机构颁发的(注意这种情况并不一定说明有SSL劫持发生)
2、证书过期
3、访问的网站域名与证书绑定的域名不一致

至此，可以知道证书在一定程度上是非常安全的，客户端只要收到的证书是合法的，就能很大程度上保证整个会话是安全的。

客户端具体是如何验证SSL证书的

为了抵御这种中间人攻击，SSL证书需要由可信的SSL证书颁发机构颁发，形成一个证书链（比如Gmail的证书链为：最底层为网域 mail.google.com，上一层为Thawte SGC CA证书颁发机构，最顶层为很有名的VeriSign证书颁发机构）。那么，浏览器除了需要验证域和有效期外，还要检查证书链中的上级证书公钥是否有效，上级的上级证书公钥是否有效，直至根证书公钥为止。这样就可以有效避免中间人攻击了，因为根证书公钥都是预装在操作系统中的，黑客如果不是暴力破解，无法得到根证书的私钥。如果黑客自己生成一个私钥，浏览器验证根证书公钥的时候发现无法通过操作系统中预装的公钥加密数据后使用这个私钥进行解密，从而判定这个公钥是无效的。这个方案也是现在https通讯通常的方案。

那么，这个现在所有的浏览器正在使用的https通讯方案就无懈可击了吗？答案仍是否定的。我们可以看到，在后一个方案中，https的安全性需要在证书颁发机构公信力的强有力保障前提下才能发挥作用。如果证书颁发机构在没有验证黑客为mail.google.com的持游者的情况下，给黑客颁发了网域为mail.google.com的证书，那么黑客的中间人攻击又可以顺利实施然而，不验证域名持有者就颁发证书的情况在国外几乎不会发生，但是在国内就不一定了。针对破解目标，国内证书颁发机构WoSign（在此只是举例国内比较有名的证书颁发机构WoSign，并不代表WoSign今后一定会这么做）很有可能为了上级要求颁发了证书给非域名持有者的黑客，从而使得破解目标的Gmail密码被黑客截取。

涉及到的算法

非对称加密算法：RSA，DSA/DSS
对称加密算法：AES，RC4，3DES
HASH算法：MD5，SHA1，SHA256

总结

整个过程是递进的，一步一步了解https安全的原理。

https如何保证安全又高效？
https使用非对称加密算法来交换对称加密的密钥，最后使用对称加密算法来进行通信。
如何保证非对称加密时的安全性？
服务端发送证书来传递非对称加密的公钥。保证了公钥和私钥的保密性。
客户端怎么知道证书是不是真的？
客户端根据CA证书的公钥校验证书的数字签名来保证其合法性。
客户端的CA证书不会被伪造或泄露吗？
CA证书是默认预装到浏览器和操作系统中的，所以CA证书的公钥是安全的。

Reference

http://op.baidu.com/2015/04/https-s01a01/
https://cipherstuff.wordpress.com/
http://oncenote.com/2014/10/21/Security-1-HTTPS/
http://www.williamlong.info/archives/2058.html
http://www.ruanyifeng.com/blog/2014/02/ssl_tls.html

LeetCode - Perfect Squares

发表于 3月 27 2016 更新于 8月 25 2019 Valine：

Problem Description：

Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, …) which sum to n.
For example, given n = 12, return 3 because 12 = 4 + 4 + 4; given n = 13, return 2 because 13 = 4 + 9.

Solution:

Solution1:

Dynamic Programming
Time Complexity: O(n*sqrt(n))
Space: O(n)

Solution2:

Number Theory

Legendre’s three-square theorem
Lagrange’s four-square theorem

Time Complexity: O(sqrt(n))
Space: O(1)

Code

package com.zane.algorithm.leetcode;

/**
 * Author: luojinping
 * Date: 15/9/23
 * Time: 17:23
 * <p/>
 * <p/>
 * Given a positive integer n, find the least number of perfect square numbers
 * (for example, 1, 4, 9, 16, ...) which sum to n.
 * For example, given n = 12, return 3 because 12 = 4 + 4 + 4; given n = 13,
 * return 2 because 13 = 4 + 9.
 */
public class PerfectSquares_279 {
    /**
     * cannot use greedy algorithm, counter example：
     * 98=81+16+1=49+49
     * 101=100+1=49+1+49+2
     * 7=4+1+1+1
     * 12=4+4+4=9+1+1+1
     * 思路:
     * 使用DP, dp[]数组记录历史使用最少平方数的情况.例如dp[5]=2,记录的是使用最少(1+4)平方数的数量,即2.
     *
     * @param n
     * @return
     */
    public int numSquares(int n) {
        if (n <= 2) {
            return n;
        }

        // record the least number of perfect numbers when index = i
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 2;

        for (int i = 3; i <= n; i++) {
            int leastNum = i;

            for (int j = 1; j * j <= i; j++) {
                leastNum = Math.min(leastNum, dp[i - j * j] + 1);

            }
            dp[i] = leastNum;
        }

        return dp[n];
    }


    private boolean isSquare(int n) {
        int sqrt_n = (int) (Math.sqrt(n));
        return (sqrt_n * sqrt_n == n);
    }

    /**
     * Legendre's three-square theorem:
     * The three squares theorem tells you that a positive integer n can be represented as the sum
     * of 3 squares (n = x^2 + y^2 + z^2) if and only if it is not of the form n = 4^a * (8 * b+7)
     * <p/>
     * Lagrange's four-square theorem:
     * Every natural number can be represented as the sum of four integer squares:
     * n= a^2 + b^2 + c^2 + d^2
     * <p/>
     * <p/>
     * So the are only 4 possible results: 1, 2, 3, 4.
     * <p/>
     * Refer:
     * https://leetcode.com/discuss/58056/summary-of-different-solutions-bfs-static-and-mathematics
     */
    public int numSquaresByMath(int n) {
        // If n is a perfect square, return 1.
        if (isSquare(n)) {
            return 1;
        }

        // The result is 4 if and only if n can be written in the
        // form of 4^k*(8*m + 7). Please refer to
        // Legendre's three-square theorem.
        while ((n & 3) == 0) // n%4 == 0
        {
            n >>= 2;
        }
        if ((n & 7) == 7) // n%8 == 7
        {
            return 4;
        }

        // Check whether 2 is the result.
        int sqrt_n = (int) (Math.sqrt(n));
        for (int i = 1; i <= sqrt_n; i++) {
            if (isSquare(n - i * i)) {
                return 2;
            }
        }

        return 3;
    }

    public static void main(String[] args) {
        PerfectSquares_279 perfectSquares279 = new PerfectSquares_279();
        System.out.println(perfectSquares279.numSquares(4));
        System.out.println(perfectSquares279.numSquares(7));
        System.out.println(perfectSquares279.numSquares(12));
        System.out.println(perfectSquares279.numSquares(61));
        System.out.println(perfectSquares279.numSquares(100));
        System.out.println(perfectSquares279.numSquares(101));
    }
}

Reference

https://leetcode.com/discuss/58056/summary-of-different-solutions-bfs-static-and-mathematics

LeetCode - The Skyline Problem

发表于 3月 26 2016 更新于 8月 25 2019 Valine：

Problem Description

A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Now suppose you are given the locations and height of all the buildings as shown on a cityscape photo (Figure A), write a program to output the skyline formed by these buildings collectively (Figure B).

Buildings Skyline Contour
The geometric information of each building is represented by a triplet of integers [Li, Ri, Hi], where Li and Ri are the x coordinates of the left and right edge of the ith building, respectively, and Hi is its height. It is guaranteed that 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX, and Ri - Li > 0. You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

For instance, the dimensions of all buildings in Figure A are recorded as: [ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] .

The output is a list of “key points” (red dots in Figure B) in the format of [ [x1,y1], [x2, y2], [x3, y3], … ] that uniquely defines a skyline. A key point is the left endpoint of a horizontal line segment. Note that the last key point, where the rightmost building ends, is merely used to mark the termination of the skyline, and always has zero height. Also, the ground in between any two adjacent buildings should be considered part of the skyline contour.

For instance, the skyline in Figure B should be represented as:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ].

Notes:

The number of buildings in any input list is guaranteed to be in the range [0, 10000].
The input list is already sorted in ascending order by the left x position Li.
The output list must be sorted by the x position.
There must be no consecutive horizontal lines of equal height in the output skyline. For instance, […[2 3], [4 5], [7 5], [11 5], [12 7]…] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: […[2 3], [4 5], [12 7], …]

problem link:
https://leetcode.com/problems/the-skyline-problem/

Solution

public class TheSkylineProblem_218 {
    public List<int[]> getSkylineSimpleSolution(int[][] buildings) {
        List<int[]> result = new ArrayList<>();
        List<int[]> height = new ArrayList<>();

        // height < 0: the height of building started
        // height > 0: the height of building ended
        for (int[] b : buildings) {
            height.add(new int[]{b[0], -b[2]});
            height.add(new int[]{b[1], b[2]});
        }

        // sorted by x value, if x equals then sorted by y value
        Collections.sort(height, (a, b) -> {
            if (a[0] != b[0])
                return a[0] - b[0];
            return a[1] - b[1];
        });

        // record the height of visited buildings by reverse order
        Queue<Integer> pq = new PriorityQueue<>((a, b) -> (b - a));
        pq.offer(0);

        int prevHeight = 0;
        for (int[] h : height) {
            if (h[1] < 0) {
                // save the height of building
                pq.offer(-h[1]);
            } else {
                // remove the height of building
                pq.remove(h[1]);
            }

            int curHeight = pq.peek();

            if (prevHeight != curHeight) {
                // find the turn point
                result.add(new int[]{h[0], curHeight});
                prevHeight = curHeight;
            }
        }
        return result;
    }
}

算法解释

算法思路

遍历所有的点，height用来存放每个顶点，左顶点的高度转为负数，右顶点的高度仍然是正数
对height数组排序，首先按x的值排序，当x的值相等时按z排序，这样保证了即使矩形的起点一样，也是最先处理最高的点。对于[{1,2,1},{1,2,2},{1,2,3}]这样的情况会优先处理{1,2,3}这个点。
使用优先级队列pq来保存当前最近buildings的高度，这个结构很重要！
遍历height数组，碰到左顶点时，将高度放入pq中，否则，碰到右顶点时则将高度从pq从移除。这样做的好处是，每次走完一个矩形时，高度能回归到之前的buildings的高度。
获取当前的最高高度，因为如果比当前矮的话，是不需要放入拐点中的，这点很重要！
如果当前的最高高度和之前的高度不一致，说明出现了拐点。**如果当前的最高高度矮于之前的值，说明之前的很高的建筑遇到了它的右顶点从而被移除了，所以目前的最高高度即使矮于之前的点，但是是新的隔离的building了，所以可以加入。那么如果高呢？当前高度比之前高，那肯定会是拐点了。

总结

几个关键点：

对顶点进行排序保存，对左右顶点根据正负号来加以区分
使用一个优先级队列来保存目前最高的建筑
碰到右顶点时消除目前的建筑高度
根据之前的高度和处理目前顶点以后(可能是加入了高度也可能是消除了之前的高度)的高度，对两者进行比较来找到拐点

Reference

https://leetcode.com/discuss/54201/short-java-solution

扔鸡蛋测楼层

发表于 3月 3 2016 更新于 8月 25 2019 Valine：

扔瓶子测楼层

一栋楼有n层，需要测试某种材质的玻璃瓶从哪一层掉下来恰好会碎。现在仅有两个这样的瓶子。请问怎样仍才能最快的测出楼层的临界值？

A. 只用一个瓶子从第一层扔到第n层

找到临界值的扔瓶子次数的期望为每一层的期望次数之和

1	E(x) = 1/n * 1 + 1/n * 2 + 1/n * 3 + ... + 1/n * n = (1+n)/2

所以时间复杂度是O(n)

B. 用贪心的思维

第一个瓶子从第1层开始扔，每次层数翻倍，依次为，1，2，4，8，16，直至在第 2^k 层碎掉。
第二个瓶子从第 2^(k-1) 层开始扔，直至第 2^k 层为止，中间肯定能找到临界值。
所以时间复杂度是O(lgn)

C. 用二分法

第一个瓶子每次以(i, j)为区间，扔的位置为(i+j)/2, 初始情况, i=0,j=n, 如果瓶子没碎，则i=j，直至碎掉。
第二个瓶子从第 i 层开始扔，直至第 j 层为止，中间肯定能找到临界值。

对于第 i 层，扔的情况为：

第一个瓶子：n/2, $/2+n/4 i, n/2+n/4+n/8
第二个瓶子：n/2+n/4, (n/2+n/k+1), …, i

显而易见，时间复杂度是O(n)

D. 数学推算

这个题目是需要最快的找出临界值，可以转换为，即使在最坏的情况下，也能最快地找出临界值。

我们先假设最坏情况下，瓶子下落次数为x，即我们为了找出N，一共用瓶子做了x次的实验。

那么，我们第一次应该在哪层楼往下扔瓶子呢？

先让我们假设第一次是在第y层楼扔的瓶子，如果第一个瓶子在第一次扔就碎了，我们就只剩下一个瓶子，要用它准确地找出N，只能从第一层向上，一层一层的往上测试，直到它摔坏为止，答案就出来了。

由于第一个瓶子在第y层就摔破了，所以最坏的情况是第二个瓶子要把第1到第y-1层的楼都测试一遍，最后得出结果，噢，原来瓶子在第y-1层才能摔破(或是在第y-1层仍没摔破，答案就是第y层。) 这样一来测试次数是1+(y-1)=x，即第一次测试要在第x层。

OK，那如果第一次测试鸡蛋没摔破呢，那N肯定要比x大，要继续往上找，需要在哪一层扔呢？我们可以模仿前面的操作，如果第一个瓶子在第二次测试中摔破了，那么第二个瓶子的测试次数就只剩下x-2次了(第一个瓶子已经用了2次)。这样一来，第二次扔瓶子的楼层和第一次扔瓶子的楼层之间就隔着x-2层。

我们再回过头来看一看，第一次扔瓶子的楼层在第x层，第1层到第x层间共x层；第1次扔鸡蛋的楼层到第2次扔瓶子的楼层间共有x-1层(包含第2次扔瓶子的那一层)，同理继续往下，我们可以得出，第2次扔瓶子的楼层到第3次扔瓶子的楼层间共有x-2层，最后把这些互不包含的区间数加起来，应该大于等于总共的楼层数量100，即

1
2
3

x + (x-1) + (x-2) + ... + 1 >= 100
(x+1)*x/2 >= 100
得出答案是14

即我先用第1个瓶子在以下序列表示的楼层数不断地向上测试，直到它摔破。再用第2个瓶子从上一个没摔破的序列数的下一层开始，向上测试，即可保证在最坏情况下也只需要测试14次，就能用2个瓶子找出从哪一层开始，往下扔鸡蛋，瓶子就会摔破。

1	14, 27, 39, 50, 60, 69, 77, 84, 90, 95, 99, 100

E. DP的解法

假设f(n)表示从第n层楼扔下鸡蛋，没有摔碎的最少尝试次数。第一个鸡蛋，可能的落下位置[1,n],第一个鸡蛋从第i层扔下，有两种情况：

碎了，第二个鸡蛋，需要从第一层开始试验，有i-1次机会
没碎，两个鸡蛋，还有n-i层。这个就是子问题了f(n-i)

所以，当第一个鸡蛋，由第i个位置落下的时候，要尝试的次数为 1 + max{i - 1, f(n - i)}，那么对于每一个i，尝试次数最少的，就是f(n)的值。
状态转移方程如下：

1	f(n) = min{1 + max{i - 1, f(n - 1)}}

其中: i的范围为[1, n], f(1) = 1.

F. 推广到一般化的问题

为n层楼，m个鸡蛋。
如下分析：假设f(n,m)表示n层楼、m个鸡蛋时找到最高楼层的最少尝试次数。当第一个鸡蛋从第i层扔下，有两种情况：

碎了，还剩m-1个鸡蛋，为确定下面楼层中的安全楼层，还需要f(i-1,m-1)次，找到子问题
不碎，上面还有n-i层，还需要f(n-i,m)次，又一个子问题。

状态转移方程如下：

1	f(n, m) = min{1 + max{f(n - 1, m - 1), f(n - i, m)}}

其中： i为[1, n], f(i, 1) = 1

Reference

http://www.cricode.com/3558.html
https://gist.github.com/sing1ee/5971946

快排算法

发表于 2月 27 2016 更新于 8月 25 2019 Valine：

快速排序的思路

algorithm quicksort(A, lo, hi) is
    if lo < hi then
        p := partition(A, lo, hi)
        quicksort(A, lo, p – 1)
        quicksort(A, p + 1, hi)

快速排序的partition方式

一种是Lomuto partition scheme，另外一种是Hoare partition scheme。

Lomuto partition

This scheme is attributed to Nico Lomuto and popularized by Bentley in his book

lomuto的partition实现方式

i指示最前面的大于pivot的元素位置，j从前往后滑动来调整元素位置。每次j碰到小于pivot的元素，则swap i位置的元素和j位置的元素，再i指向下一个大于pivot的元素。
最后，记得swap i位置的元素和最末尾的元素。

private int lomutoPartition(int nums[], int lo, int hi) {
        int pivot = nums[hi];
        int i = lo;
        for (int j = lo; j < hi; j++) {
            if (nums[j] <= pivot) {
                swap(nums, i, j);
                i++;
            }
        }

        swap(nums, i, hi); // replace the guard element
        return i;
    }

Hoare partition scheme

The original partition scheme described by C.A.R. Hoare uses two indices that start at the ends of the array being partitioned, then move toward each other, until they detect an inversion.

Hoare’s scheme is more efficient than Lomuto’s partition scheme because it does three times fewer swaps on average, and it creates efficient partitions even when all values are equal.

hoare的partition实现方式

i从前往后找到大于pivot的元素，j从后往前找到小于pivot的元素，然后两者swap.

private int hoarePartition(int nums[], int lo, int hi) {
        int pivot = nums[lo];
        int i = lo, j = hi;
        while (true) {
            while (nums[i] < pivot) {
                i++;
            }

            while (nums[j] >= pivot) {
                j--;
            }

            if (i >= j) {
                return j;
            }

            swap(nums, i, j);
        }
    }

硬币找零问题

发表于 2月 20 2016 更新于 8月 25 2019 Valine：

硬币找零问题(Coin Change)

Question

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

Example 1:
coins = [1, 2, 5], amount = 11
return 3 (11 = 5 + 5 + 1)

Example 2:
coins = [2], amount = 3
return -1.

Note:
You may assume that you have an infinite number of each kind of coin.

DP求解

如果是用DP求解，那么思路首先就是找到子问题。子问题很容易确定，那就是amount-x是子问题的amount。比较容易想到的代码实现如下：

public int coinChange(int[] coins, int amount) {
        if (amount == 0)
            return 0;
        int n = amount + 1; // the answer must smaller than [amount+1], nice!
        for (int coin : coins) {
            int curr = 0;
            if (amount >= coin) {
                int next = coinChange(coins, amount - coin);
                if (next >= 0)
                    curr = 1 + next;
            }
            if (curr > 0)
                n = Math.min(n, curr);
        }
        return (n == amount + 1) ? -1 : n;
    }

上述算法的时间复杂度为O(c^n),c是coin的数量，n是amount的值。

时间复杂度较大的原因是，中间存在很多重复计算。那么需要用到DP的备忘录，不用全局变量来保存计算过的值，也不用递归的方法来实现，而是只用一个一维数组，再用循环来实现。代码如下：

public int coinChange(int[] coins, int amount) {
        if (coins == null || coins.length == 0 || amount <= 0)
            return 0;
        int[] minNumber = new int[amount + 1];
        for (int i = 1; i <= amount; i++) {
            minNumber[i] = amount + 1;
            for (int j = 0; j < coins.length; j++) {
                if (coins[j] <= i && minNumber[i - coins[j]] != amount + 1)
                    minNumber[i] = Integer.min(minNumber[i], 1 + minNumber[i - coins[j]]);
            }
        }
        if (minNumber[amount] == amount + 1)
            return -1;
        else
            return minNumber[amount];
    }

判断图是否为树

发表于 2月 2 2016 更新于 8月 25 2019 Valine：

题目

输入二维数组，a[i][j]=1 表示从i结点指向j结点。

eg1

0 1 1 0

1 0 0 1

1 0 0 0

0 1 0 0

是一棵树，树为：

eg2

0 1 1 0

1 0 0 1

1 0 1 0

0 1 1 0

不是一颗树，是有环(a-b-d-c-a)的图：

关键点

判断一张图是否是一颗树的两个关键点：

不存在环路(对于有向图，不存在环路也就意味着不存在强连通子图)
满足边数加一等于顶点数的规律(不考虑重边和指向自身的边)

方法

DFS
如果存在回路，则必存在一个子图，是一个环路。环路中所有顶点的度>=2。时间复杂度O(ve)，v是顶点数，e是边数。
第一步：删除所有度<=1的顶点及相关的边，并将另外与这些边相关的其它顶点的度减一。
第二步：将度数变为1的顶点排入队列，并从该队列中取出一个顶点重复步骤一。如果最后还有未删除顶点，则存在环，否则没有环。这个复杂度也很高
结合树的特性(边数+1 = 顶点数)和并查集来做，代码见下文。

实现

import java.util.ArrayList;
import java.util.List;

public class TreeJudgeUnionB {
    private static class Edge {
        int start;
        int end;

        public Edge(int start, int end) {
            this.start = start;
            this.end = end;
        }
    }

    // the number of edges
    private int n;

    // edge list
    private List<Edge> edges = new ArrayList<>();

    // the index of group
    private int[] group;

    // the size of tree
    private int[] size;

    public TreeJudgeUnionB(int n, List<Edge> edges) {
        this.n = n;
        this.edges = edges;

        group = new int[n];
        size = new int[n];
        for (int i = 0; i < n; i++) {
            group[i] = i;
            size[i] = 1;
        }
    }

    private int find(int i) {
        // find the root of a tree which contains i node
        while (i != group[i]) {
            i = group[i];
        }

        return i;
    }

    private boolean union(int groupI, int groupJ) {
        int iRoot = find(groupI);
        int jRoot = find(groupJ);
        if (iRoot != jRoot) {
            if (size[iRoot] < size[jRoot]) {
                group[iRoot] = jRoot;
                size[jRoot] += size[iRoot];
            } else {
                group[jRoot] = iRoot;
                size[iRoot] += size[jRoot];
            }

            return true;
        } else {
            return false;
        }
    }

    public boolean isTree() {
        for (Edge edge : edges) {
            if (!union(edge.start, edge.end)) {
                System.out.println("input two nodes in the same tree");
                return false;
            }
        }

        boolean hasRoot = false;
        for (int i = 0; i < group.length; i++) {
            if (i == group[i]) {
                if (!hasRoot) {
                    hasRoot = true;
                } else {
                    System.out.println("exist more than one tree root");
                    return false;
                }
            }
        }

        printGroup();

        return hasRoot;

    }

    public void printGroup() {
        for (int i = 0; i < n; i++) {
            System.out.print(group[i] + ", ");
        }
        System.out.println();
    }


    public static void main(String[] args) {
        int n = 5;
        List<Edge> edges = new ArrayList<>();
        addEdge(edges, 0, 1);
        addEdge(edges, 0, 2);
        addEdge(edges, 2, 3);
        addEdge(edges, 2, 4);
        isTree(n, edges); // true

        n = 5;
        edges.clear();
        addEdge(edges, 0, 1);
        addEdge(edges, 1, 2);
        addEdge(edges, 0, 2);
        addEdge(edges, 2, 3);
        addEdge(edges, 2, 4);
        isTree(n, edges); // false

        n = 4;
        edges.clear();
        addEdge(edges, 0, 1);
        addEdge(edges, 2, 3);
        isTree(n, edges);  // false

        n = 7;
        edges.clear();
        addEdge(edges, 0, 1);
        addEdge(edges, 1, 2);
        addEdge(edges, 4, 5);
        addEdge(edges, 3, 4);
        addEdge(edges, 2, 3);
        addEdge(edges, 0, 6);
        isTree(n, edges);  // true
    }

    protected static void addEdge(List<Edge> edges, int i, int j) {
        edges.add(new Edge(i, j));
    }

    protected static void isTree(int n, List<Edge> edges) {
        TreeJudgeUnionB treeJudgeUnionA = new TreeJudgeUnionB(n, edges);

        boolean isTree = treeJudgeUnionA.isTree();

        System.out.println("This is a tree? " + isTree);
    }
}

并查集(Union-Find)算法

发表于 2月 2 2016 更新于 8月 25 2019 Valine：

介绍

在计算机科学中，并查集是一种树型的数据结构，其保持着用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。有一个联合-查找算法（union-find algorithm）定义了两个操作用于此数据结构：

Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。

Union：将两个子集合并成同一个集合。

适用场景

适合于判断，给出一组结点，判断他们是否联通。

实现思路

建立n个分组，每个分组代表一堆可以互相联通的结点。
遍历每对结点，找到他们各自所属的分组A, B
如果A != B，则将A, B分组union起来，表示A, B分组联通了
如果A == B，则跳过

Simple Find 操作

用 group[] 数组来判断某个id属于的组。初始状态时，每个id都属于不同的组。

1 2	for(int i = 0; i < size; i++) group[i] = i;

Simple Union 操作

public void union(int p, int q) {   
  // get the groupId of every node
  int pId = find(p);  
  int qId = find(q);  
  
  // the two nodes are connected, return
  if (pId == qId) {
    return;  
  }
  
  // union the two nodes, change groupId
  for (int i = 0; i < id.length; i++) {
      if (group[i] == pId) {
        group[i] = qId;  
      }
  }
}

优化

上面最后一步的union操作存在性能问题，即每次都需要改变其中一个分组中的所有结点的分组id。优化的做法是，用一颗树来表示每个分组，树的根节点表示当前组的id。

但如果用树来表示会引入一个问题，即可能存在树退化为链表的情况，这样一来，每一次加入一个结点再找根结点也会很耗时，没有达到优化的目的。
针对树可能退化为链表的解决方案是，每次合并树时，总是将矮的树挂到高的树下。这种方式也称为「按秩合并」

除了使用树来优化union性能以外，还有一种方式，称为「路径压缩」，即 Find 递归地经过树，改变每一个节点的引用到根节点。得到的树将更加扁平，为以后直接或者间接引用节点的操作加速。

总结：

使用树来存储分组，Union时「按秩合并」
「路径压缩」，Find时改变每一个节点的引用到根节点

Find 操作

1
2
3

// store every tree's size
for (int i = 0; i < N; i++)  
    size[i] = 1;

private int find(int p)  
{    
  if(p != group[p]){
    group[p] = find(group[p])
  }
    
  return group[p]
}

Union 操作

public void union(int p, int q)
{
	int i = find(p);
	int j = find(q);
	
	if (i == j) {
	  return;
	} 
	
	if (size[i] < size[j]) { 
	  group[i] = j; 
	  size[j] += size[i]; 
	}	else { 
	  group[j] = i; 
	  size[i] += size[j]; 
	}
}

时间复杂度

Statement: If m operations, either Union or Find, are applied to n elements, the total run time is O(m logn), where log is the iterated logarithm.
Proof of O(logn) time complexity of union-find: https://en.wikipedia.org/wiki/Proof_of_O\(logn)_time_complexity_of_union%E2%80%93find

Reference

https://zh.wikipedia.org/wiki/%E5%B9%B6%E6%9F%A5%E9%9B%86
http://blog.csdn.net/dm_vincent/article/details/7655764
https://en.wikipedia.org/wiki/Proof_of_O(log*n)_time_complexity_of_union%E2%80%93find