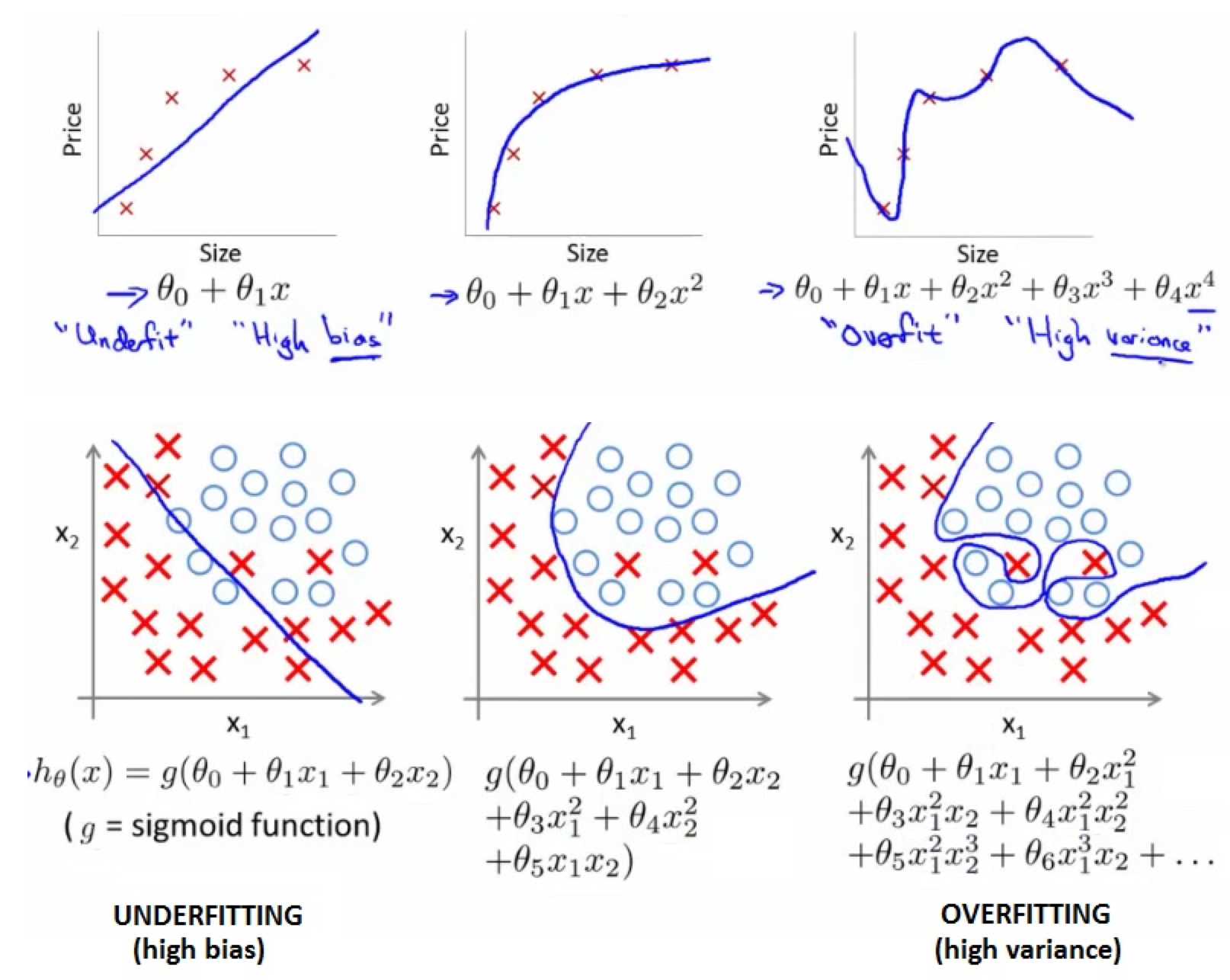
欠拟合与过拟合
欠拟合:underfitting,与训练数据贴合的不够好,不能准确预测未来目标值。
过拟合:overfitting,与训练数据贴合的太好了,预测未来目标值的准确性有较大风险。
线性模型的概率解释
思考:我们为什么要用最小二乘的指标作为 cost function?为什么不是绝对值或四次方?
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。
最小二乘是从函数形式上来看的,极大似然是从概率意义上来看的。事实上,最小二乘可以由高斯噪声假设+极大似然估计推导出来。当然极大似然估计还可以推导出其他的loss function, 比如logistic回归中,loss function是交叉熵。
最大似然估计与最小二乘估计的区别
一般的最小二乘法实际上是在假设误差项满足高斯分布且独立同分布的情况下,使似然性最大化。
推导过程
回到预测房价的例子,假设最终的预测函数,每一次预测都有误差,用$ε^{(i)}$表示误差,则预测函数可以写为:
其中,误差是随机分布的,均值为 0,服从高斯分布 $N(0,σ^2)$。
Andrew Ng 讲到在大多数情况下,线性回归的误差值如果综合来看,就是符合高斯分布的。并且根据中心极限定律,正态分布确实是对误差项分布的合理猜想。
所以
$P(y^{(i)}|x^{(i)}; θ)$ 表示:在 θ 为给定的参数的情况下,概率 $y^{(i)}$ 以 $x^{(i)}$ 为随机变量的概率分布,注意 θ 不是随机变量。
由于 ε(i) 是独立的同分布(IID:independentlyidentically distribution),所以以 θ 为变量的似然函数为:
对 L(θ) 取对数有:
最大化 $l(\theta)$ 即是最小化 $\frac1{2\sigma^2}\sum_{i=1}^{m}(y^{(i)}-\theta^Tx^{(i)})^2$,这样就是 cost function.
由于目标变量服从正态分布,但分布的均值和方差都未知,对均值和方差两个参数的合理估计是选取两个参数使得在正态分布的前提下,抽到各样本中的 y 值的概率最大,这就是最大似然估计的思想。
Reference
http://www.holehouse.org/mlclass/07_Regularization.html
http://rstudio-pubs-static.s3.amazonaws.com/4810_06e3d8fd26ed40eb8c31aff35eae81ae.html
https://rpubs.com/badbye/ml03
http://www.qiujiawei.com/linear-algebra-15/
最大似然估计
