要解决的问题
与「机器学习实战 — 决策树」的问题一样
前情回顾
在上一次中,随机森林的效果最好,最终效果如下: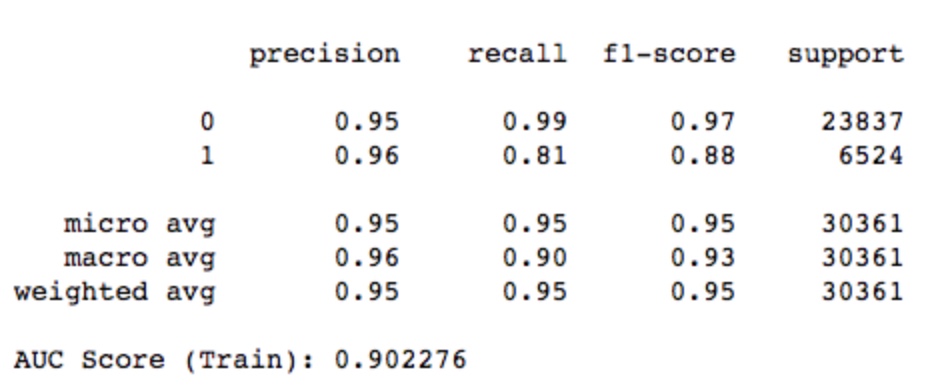
特征工程
特征工程与第二次作业一样,但增加了最后一步「特征归一化」,步骤概述如下:
- 特征选取
- 删除无用特征
- 空值处理
- 处理重要特征
- 特征标签化
- 特征归一化
特征归一化
使用 StandardScaler 和 MinMaxScaler 的差别不大,最终使用的是 StandardScaler。因为特征基本上都是符合正态分布的,而且 StandardScaler 对数据变动时引入新的极值点更友好。
1 | # 使用 z-score 标准化特征 |
特征归一化的好处有以下两点:
- 模型训练速度更快
能够使参数优化时能以较快的速度收敛。
归一化前后的 SVM(linear 核) 的耗时对比,数据集 (2783, 54),即 2783 条数据,54 个特征。归一化前后的耗时分别为:1083s,0.44s,可见归一化对计算速度的提升非常大。 - 模型的准确率提升
将特征缩放到同一尺度的量级,能够使搜索的跳跃更加平滑,避免反复震荡的情况,提高准确率。可以参考下图形象化的解释: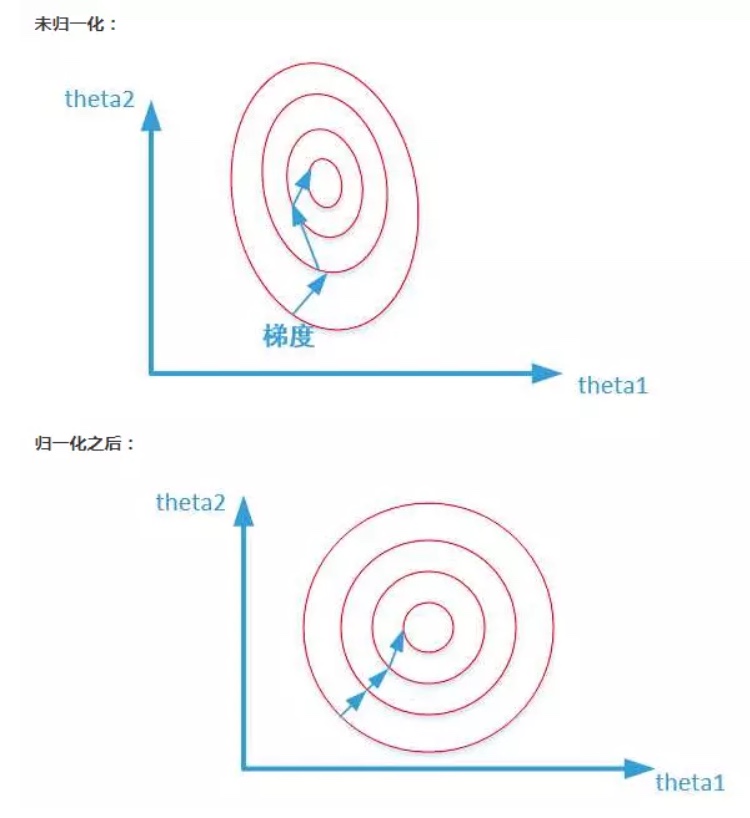
对于不同数量的训练集,训练 SVM,LR,DT,RF 四个模型。随着数据集的数量增加,特征归一化后的模型,其准确率提升如下图所示: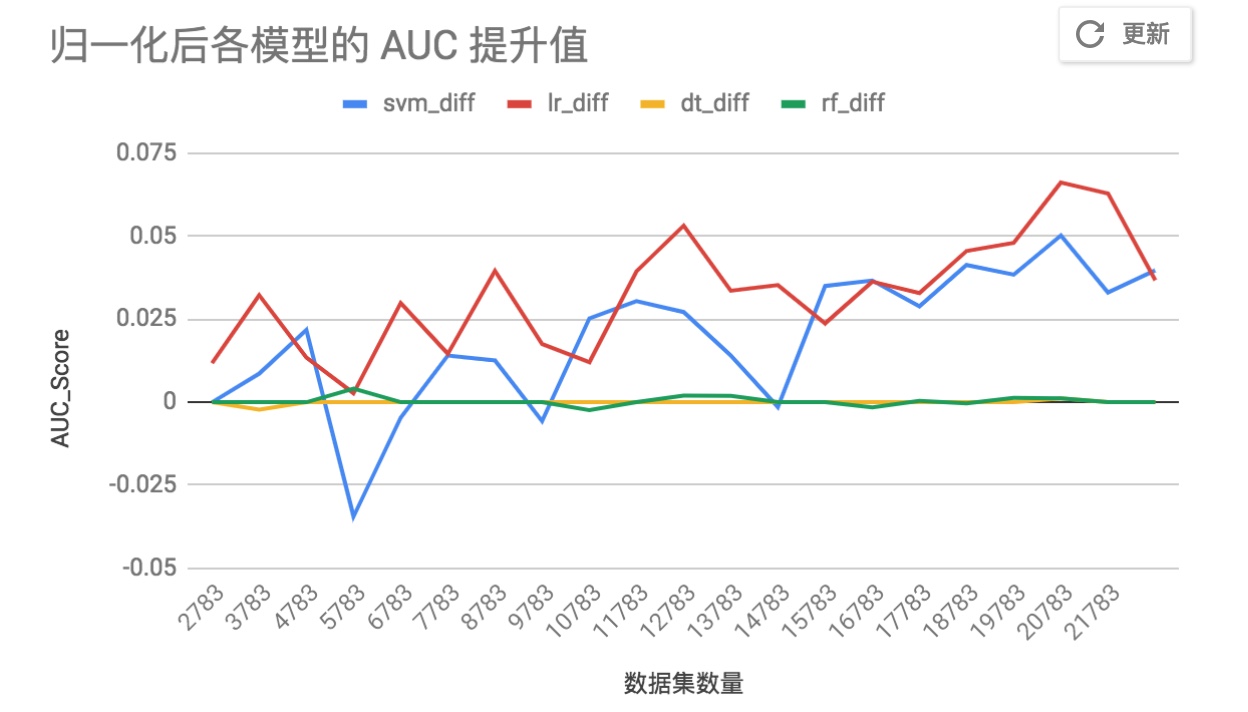
通过这个图,也会发现特征归一化也不是能够提升所有模型的准确率,对于 DT 和 RF 就没有效果,这是因为决策树的分支只是计算信息熵,而不考虑整体特征的分布情况。
最终数据集
经过一系列处理后可用的数据集有 30w,但由于 SVM 运行地太慢了,从中选取 2w 数据来作为本次作业的数据集。
SVM
核函数介绍
常见的核函数有:
- linear:主要用于线性可分的情形。参数少,速度快,对于一般数据,分类效果已经很理想了。
- rbf:将样本映射到更高维的空间,目前应用最广的一个,对大小样本都有比较好的性能,而且参数较少。linear 是 rbf 的一个特例。
- poly:多项式核函数,将低维的输入空间映射到高纬的特征空间,参数多,当多项式的阶数比较高时,计算复杂度会非常大。
- sigmod:支持向量机实现的就是一种多层神经网络。
Andrew Ng 的建议:
- 如果Feature的数量很大,跟样本数量差不多,这时候选用LR或者是Linear Kernel的SVM
- 如果Feature的数量比较小,样本数量一般,不算大也不算小,选用SVM+Gaussian Kernel
- 如果Feature的数量比较小,而样本数量很多,需要手工添加一些feature变成第一种情况
本次作业的数据集特征少,数据大。结合上述建议,再加上取了少部分(1k~5k)的数据进行了初步对比,决定重点调优 rbf 的参数。
SVM RBF 参数搜索
训练集数据量: 2w。搜索最优参数,用时 12.3 小时,将 搜索过程的数据记录 绘制成下图所示,纵轴代表搜索得分,横轴代表 {C, gamma} 两个参数的取值。
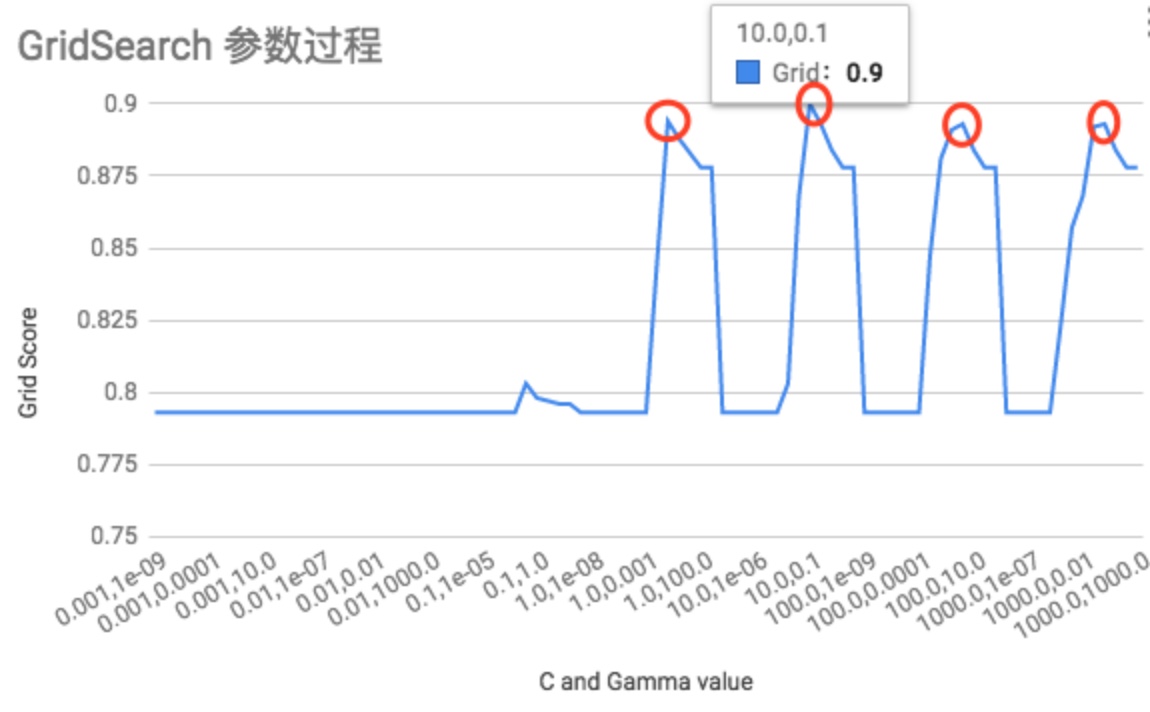
C = 10, gamma = 0.1 时的效果最好。如上图中红圈所示,对于 C = 0.1, 100, 1000 时,都是gamma = 0.1 这个位置时效果最好。
常用核函数
在本次作业的数据集中,linear 核函数的运算速度相当慢,所以对于常用核函数,仅对比了 rbf,poly 和 sigmoid 三个核函数。针对 2w 条数据,运行结果如下:
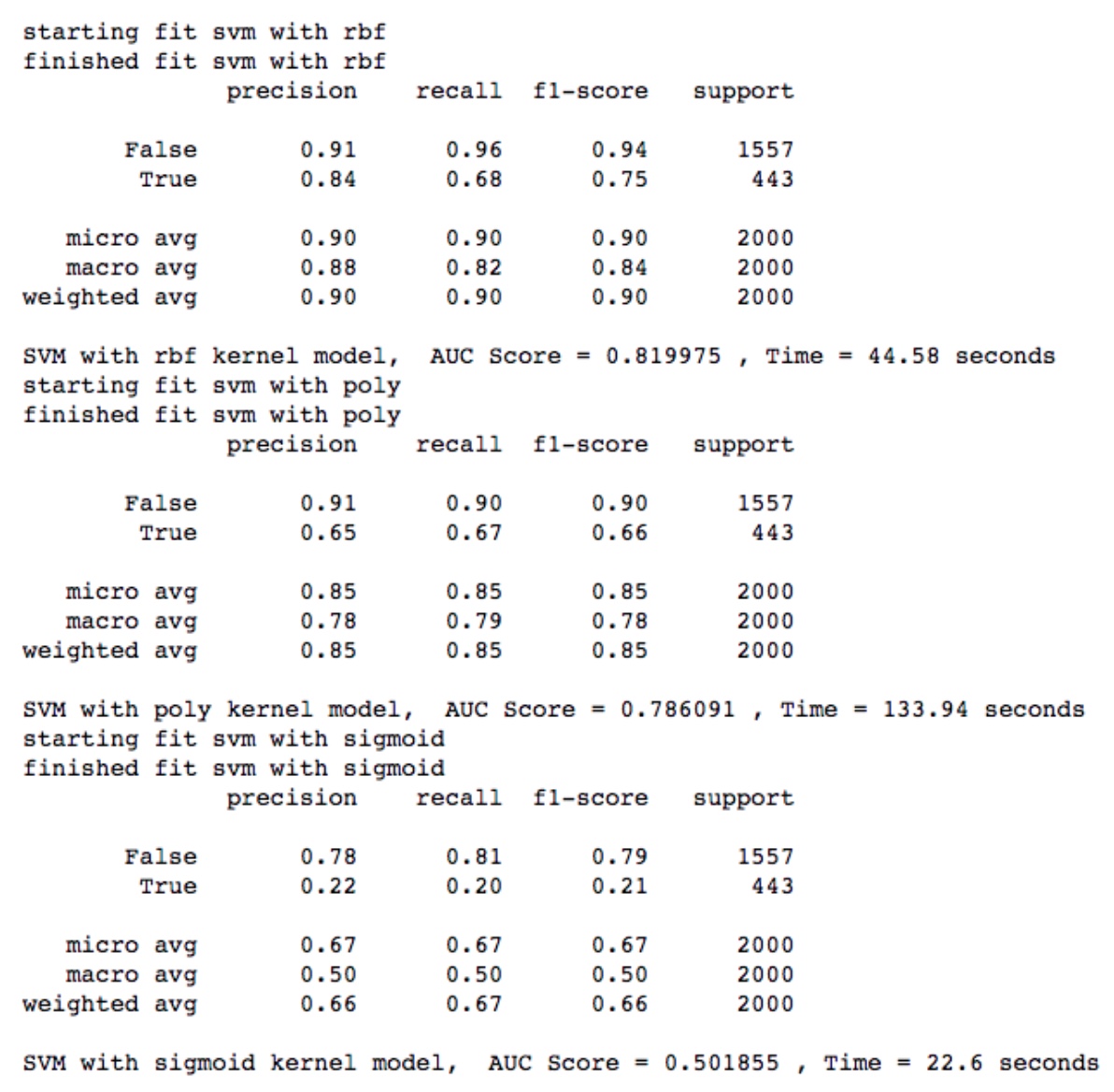
其中,rbf 效果最好,AUC 有 0.82,但相比起之前 AUC 0.9 的 RF 来还是不理想。
自定义核函数
由于常用核函数的效果不够理想,所以尝试使用自定义的核函数,参考前人总结出的各种核函数,放入模型中进行尝试。核函数的公式见原代码,任取两个核函数的说明如下:
Rational quadratic kernel1
2
3
4
5
6
7
8
9
10"""
Rational quadratic kernel,
K(x, y) = 1 - ||x-y||^2/(||x-y||^2+c)
where:
c > 0
"""
def rational_quadratic(data_1, data_2):
_c = 1
dists_sq = euclidean_dist_matrix(data_1, data_2)
return 1. - (dists_sq / (dists_sq + _c))
Inverse multiquadratic kernel1
2
3
4
5
6
7
8
9
10
11
12
13
14"""
Inverse multiquadratic kernel,
K(x, y) = 1 / sqrt(||x-y||^2 + c^2)
where:
c > 0
as defined in:
"Interpolation of scattered data: Distance matrices and conditionally positive definite functions"
Charles Micchelli
Constructive Approximation
"""
def inverse_multiquadratic(data_1, data_2):
_c = 1 ** 2
dists_sq = euclidean_dist_matrix(data_1, data_2)
return 1. / np.sqrt(dists_sq + _c)
仍然是对于这 2w 条数据,将所有核函数放入 SVM 中训练,最终每个核函数的准确率和耗时对比表格如下:
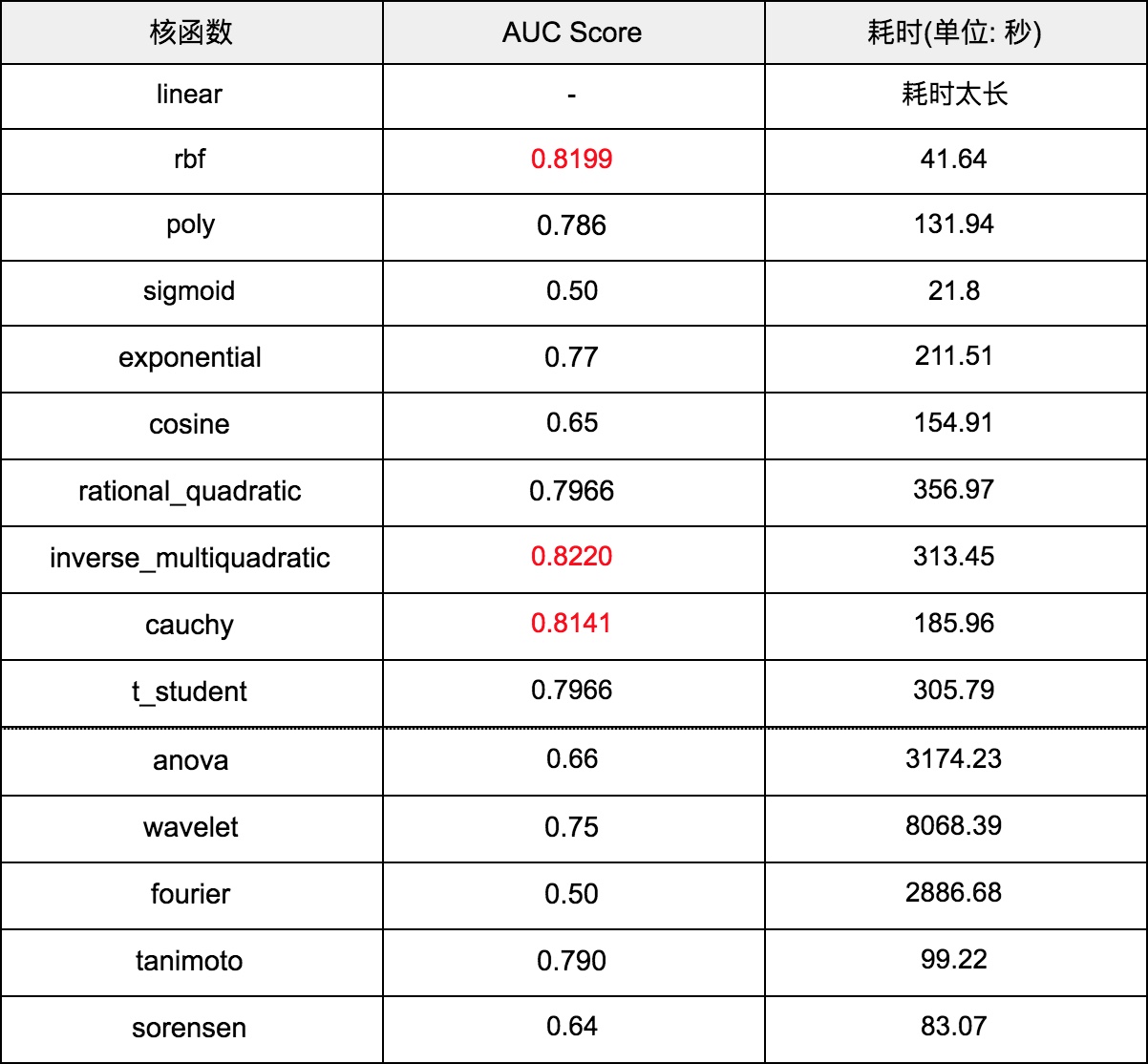
可以发现 rbf, inverse_multiquadratic 和 cauchy 这三个核函数的效果较好,其中 rbf 训练速度最快,inverse_multiquadratic 准确率最高。
总结
SVM 准确率的思考
最终,使用 inverse_multiquadratic 核函数可以将 SVM 模型的 AUC Score 最高调至 0.822,相比于第二次作业中 Random Forest 模型的 AUC Score 结果 0.902 还有差距。可能是由于核函数选取的仍然不够合适,在映射后的空间中数据不是那么线性可分,降低了模型的泛化能力,导致准确率不如 RF。而对于核函数的选取,需要更多地理解特征,并列举出所有可能的核函数,再进行对比选择,在选取核函数这一点上,没有很好的捷径可走。
提升 SVM 训练速度的心得
- 特征标签化和归一化
- SVC 的 cache_size 设置到 7000 (M)
- 核函数是 SVM 的关键,先用少部分数据来选核函数,再用全量数据训练
- SVM 的 C 参数不要设置的太大
参考文档
1.4. Support Vector Machines — scikit-learn 0.20.1 documentation
RBF SVM parameters — scikit-learn 0.20.1 documentation
逻辑斯蒂回归VS决策树VS随机森林 - 简书
https://www.csie.ntu.edu.tw/~r95162/guide.pdf
https://github.com/gmum/pykernels
