前言
线性回归出的模型如果出现过拟合怎么办?
- 脏数据太多,需要清洗数据
- 增加训练数据的数量和多样性
- 特征数量过多,使用正则化减少特征数量
向量的范数
向量的范数是一种用来刻画向量大小的一种度量。实数的绝对值,复数的模,三维空间向量的长度,都是抽象范数概念的原型。上述三个对象统一记为 x ,衡量它们大小的量记为 ||x|| (我们用单竖线表示绝对值,双竖线表示范数),显然它们满足以下三条性质:
L0范数:向量中非零元素的个数。
L1范数:向量中各个元素绝对值之和,又叫“稀疏规则算子”(Lasso regularization)
L2范数:向量中各个元素平方和再开方
p-范数:$||\textbf{x}||_p = (\sum_{i=1}^N|x_i|^p)^{\frac{1}{p}}$,即向量元素绝对值的p次方和的1/p次幂。
下图展示了 p 取不同值时 unit ball 的形状:

正则化
在统计学的缩减中,引入了惩罚项,减少了不重要的参数,同时还可采用正则化(regularization)减少不重要的参数。
既然是减少特征,那么最容易想到的就是使用 L0 范数,求回归函数中的参数向量 w 的非零元素的个数。如果约束 $‖w‖_0≤k$,就是约束非零元素个数不大于 k。不过很明显,L0 范数是不连续的且非凸的,如果在线性回归中加上 L0 范数的约束,就变成了一个组合优化问题:挑出 $≤k$ 个系数然后做回归,找到目标函数的最小值对应的系数组合,这是一个 NP 问题。
有趣的是,L1 范数也可以达到稀疏的效果,是 L0 范数的最优凸近似。我们把引入 L1 范数的线性回归叫做 Lasso 回归。
Lasso 回归
Lasso 算法(英语:least absolute shrinkage and selection operator,又译最小绝对值收敛和选择算子、套索算法)是一种同时进行特征选择和正则化(数学)的回归分析方法,旨在增强统计模型的预测准确性和可解释性,最初由斯坦福大学统计学教授 Robert Tibshirani 于 1996 年基于 Leo Breiman 的非负参数推断(Nonnegative Garrote, NNG)提出。
优化目标:min $ 1/N\ast\sum_{i = 1}^{N}{(y_{i} -\omega^{T} x_{i})^{2} }$
Lasso 回归:min $1/N\ast\sum_{i = 1}^{N}{(y_{i} -\omega^{T} x_{i})^{2} } + \lambda||\omega||_{1}$
Ridge 回归
岭回归是加了二阶正则项的最小二乘,主要适用于过拟合严重或各变量之间存在多重共线性的时候,岭回归是有 bias 的,这里的 bias 是为了让 variance 更小。
Ridge 回归:min $1/N\ast\sum_{i = 1}^{N}{(y_{i} -\omega^{T} x_{i})^{2} } + \lambda ||\omega||_{2}^{2} $
岭回归最先是用来处理特征数多与样本数的情况,现在也用于在估计中加入偏差,从而得到更好的估计。这里引入λ限制了所有w的和,通过引入该惩罚项,能够减少不重要的参数,这个技术在统计学上也叫做缩减。缩减方法可以去掉不重要的参数,因此能更好的理解数据。选取不同的λ进行测试,最后得到一个使得误差最小λ。
缩减方法可以去掉不重要的参数,因此能更好地理解数据。此外,与简单的线性回归相比,缩减法能取得更好的预测效果。
比较两者
Lasso 回归与 Ridge 回归有共同点,也有区别。
共同点
都能解决两个问题:
- 线性回归出现的过拟合现象
- 使用 Normal equation 求解时,解决 $(X^TX)$ 不可逆的问题。
区别
岭回归加入的正则项是 L2 范数,其结果可以将偏回归系数往 0 的方向进行压缩,但不会把偏回归系数压缩为 0,即岭回归不会剔除变量。Lasso 回归同样也可以将偏回归系数往 0 方向压缩,但是能够将某些变量的偏回归系数压缩为 0,因此可以起到变量筛选的作用。
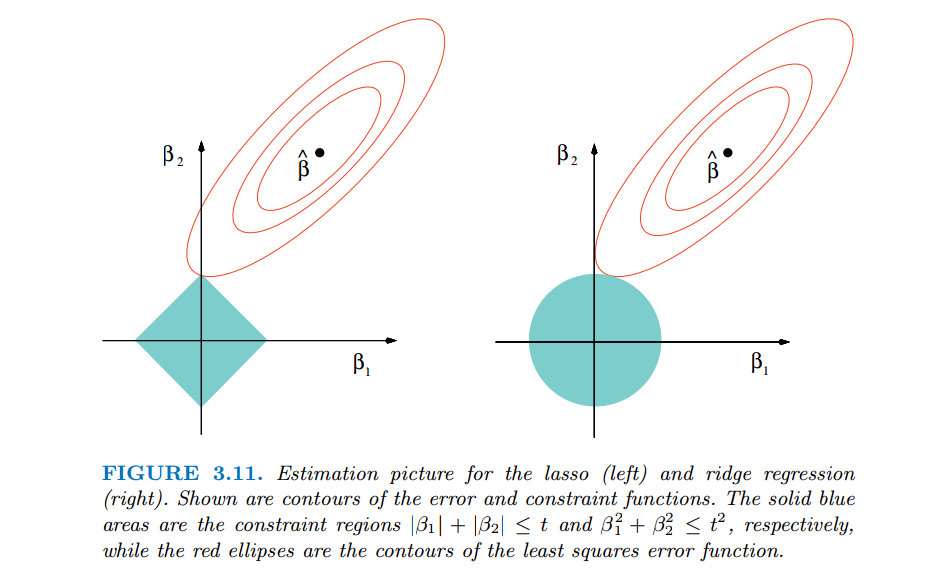
红色的椭圆和蓝色的区域的切点就是目标函数的最优解,我们可以看到,如果是圆,则很容易切到圆周的任意一点,但是很难切到坐标轴上,因此没有稀疏;但是如果是菱形或者多边形,则很容易切到坐标轴上,因此很容易产生稀疏的结果。这也说明了为什么 L1 范式会是稀疏的。
Reference
Lasso算法 - 维基百科,自由的百科全书
机器学习方法:回归(二):稀疏与正则约束ridge regression,Lasso
