SVM 定义

支持向量机，因其英文名为 support vector machine，故一般简称 SVM，通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

函数间隔和几何间隔

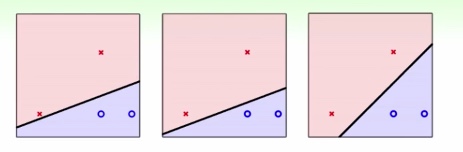
svm_margin
上图中哪个分类器最好呢？

符号定义

为了方便介绍 SVM，重新定义以下符号。

在logstic回归中我们用0,1代表两个类, 现在我们改用-1,+1, 即 y∈{-1，-1}
在logistic回归中, 我们的 g 是sigmoid函数, 现在改为:
g(z)=1, z>=0
g(z)=-1, z<0
在logistic回归中, 我们的假设函数为 $h_θ(x)$, 现在改为, $h_\theta(x)$
$h_{x,b}(x)=g(w^{T}x+b)$, 其中w相当于$[θ_1,θ_2,θ_3,…θ_n]^T$, b 相当于 $θ_0$，即截距。

h_{x,b}

$x=a+b$

函数间隔(functional margin)

对于一个训练样本 $(x^{(i)}, y^{(i)})$，我们定义它到超平面 (w,b) 的函数间隔为:

$\widehat\gamma=y^{(i)}(w^{T}x^{(i)}+b)$

我们希望函数间隔越大越好, 即:
if $y^{(i)}=1$, want $(w^{T}x^{(i)}+b) \gg 0 $ (>>代表远大于)
if $y^{(i)}=-1$, want $(w^{T}x^{(i)}+b) \ll 0$

函数间隔越大，代表我们对于分类的结果非常确定。

但这里有一个漏洞，即可以在不改变这个超平面的情况下可以让函数间隔任意大，只要我们成比增加 w,b 就可以达到这个目的了。例如，我们将 w 变为 2w， b 变为 2b，那么我们的函数间隔将会是原来的两倍。

所以对于整个训练集, 函数间隔定义为：

$\widehat\gamma=min{\widehat\gamma^{(i)}}$

几何间隔(geometric margin)

定义对于一个训练样本 $A(x^{(i)}, y^{(i)})$，它到超平面 $w^{T}x^{(i)}+b$ 的几何距离为 $\gamma^{(i)}$。
设 B 为 A 在超平面上的投影，易得超平面的法向量为 $\frac{w}{||w||}$，则有 $A=B+\gamma^{(i)}\frac{w}{||w||}$，
即 $B = A - \gamma^{(i)}\frac{w}{||w||}$。又因为 B 在超平面上，所以有
$w^{T}(x^{(i)} - \gamma^{(i)}\frac{w}{||w||})+b=0$
故几何距离为:

$\gamma^{(i)}=(\frac{w}{||w||})^{T}x^{(i)} + \frac{b}{||w||}$

定义其几何间隔：

$\gamma^{(i)}=y^{(i)}[(\frac{w}{||w||})^{T}x^{(i)} + \frac{b}{||w||}]$

所以对于整个训练集, 几何间隔定义为：

$\gamma=min{\gamma^{(i)}}$

可以发现，当 $||w||=1$时，$\widehat\gamma^{(i)}=\gamma^{(i)}$

最优间隔分类器

几何间隔就是在求 $\frac{\widehat\gamma}{||w||}$ 的最小值，可以发现函数间隔 $\widehat\gamma$ 可放大缩小，且其对结果不产生影响，所以不妨设令${\widehat\gamma}=1$。
现在，目标函数转为了：

$max \frac{1}{||w||}, s.t., y^{(i)}(w^{T}x^{(i)}+b)\ge1, i=1,2,3...,n$

等价于

$min{\frac12{||w||^2}}, s.t., y^{(i)}(w^{T}x^{(i)}+b)\ge1, i=1,2,3...,n$

利用拉格朗日乘子法可得：

$L(w,b,\alpha)=\frac12{||w||^2}-\sum_{i=1}^{n}\alpha_i[y^{(i)}(w^{T}x^{(i)}+b)-1]$

令

$\theta(w)=\displaystyle\max_{\alpha_i\ge0}L(w, b, \alpha)$

则目标函数变成了：

$\displaystyle\min_{w,b}\theta(w)=\displaystyle\min_{w,b}\max_{\alpha_i\ge0}L(w, b, \alpha)=p^\*$

求解目标函数

使用对偶问题求解

SVM 中用到了高维映射，将线性不可分的问题映射为线性可分，且映射函数的具体形式无法提前确定，而往往使用核函数映射后，维度 w 会提升很多，甚至至无穷维。
在原问题下，求解算法的复杂度与样本维度（w 的维度）相关；
在对偶问题下，求解算法的复杂度与样本数量（等于拉格朗日算子 a 的数量）相关。

因此，如果是做线性分类，且样本维度低于样本数量的话，可以在原问题下求解。例如 Liblinear 的线性 SVM 默认做法就是这样的；
但如果是做非线性分类，那就会涉及到升维（比如使用高斯核做核函数，其实是将样本升到无穷维），升维后的样本维度往往会远大于样本数量，此时显然在对偶问题下求解会更好。

直接求解原问题有多难？ TBD

使用对偶问题的解法

对于不等书约束条件的最优化问题，使用拉格朗日对偶问题来求解。具体介绍见之前的 blog: 拉格朗日乘子法

用 $p^*$ 表示这个问题的最优值，这个问题和我们最初的问题是等价的。
不过，把最小和最大的位置交换一下：

$\displaystyle\max_{\alpha_i\ge0}\min_{w,b}L(w, b, \alpha)=d^*$

交换以后的问题不再等价于原问题，新问题的最优值用 $d^$ 来表示。并且，有 $d^$ ≤ $p^*$。

第二个问题的最优值 $d^$ 提供了一个第一个问题的最优
值 $p^$ 的一个下界。经过论证，原始问题满足强对偶所需要的条件，故这两者相等，所以可以通过求解第二个问题来间接地求解第一个问题。

优化公式

要让 L 关于 w 和 b 最小化，分别对 w，b 求偏导数，即令
$\frac{∂L}{∂w}$ 和 $\frac{∂L}{∂b}$ 等于零，有：

$\frac{∂L}{∂w}=w-\sum_{i=1}^{n}\alpha_iy^{(i)}x^{(i)}=0$ $\frac{∂L}{∂b}=\sum_{i=1}^{n}\alpha_iy^{(i)}=0$

将上式代入：

$L(w,b,\alpha)=\frac12{||w||^2}-\sum_{i=1}^{n}\alpha_i[y^{(i)}(w^{T}x^{(i)}+b)-1]$

推导过程如下：
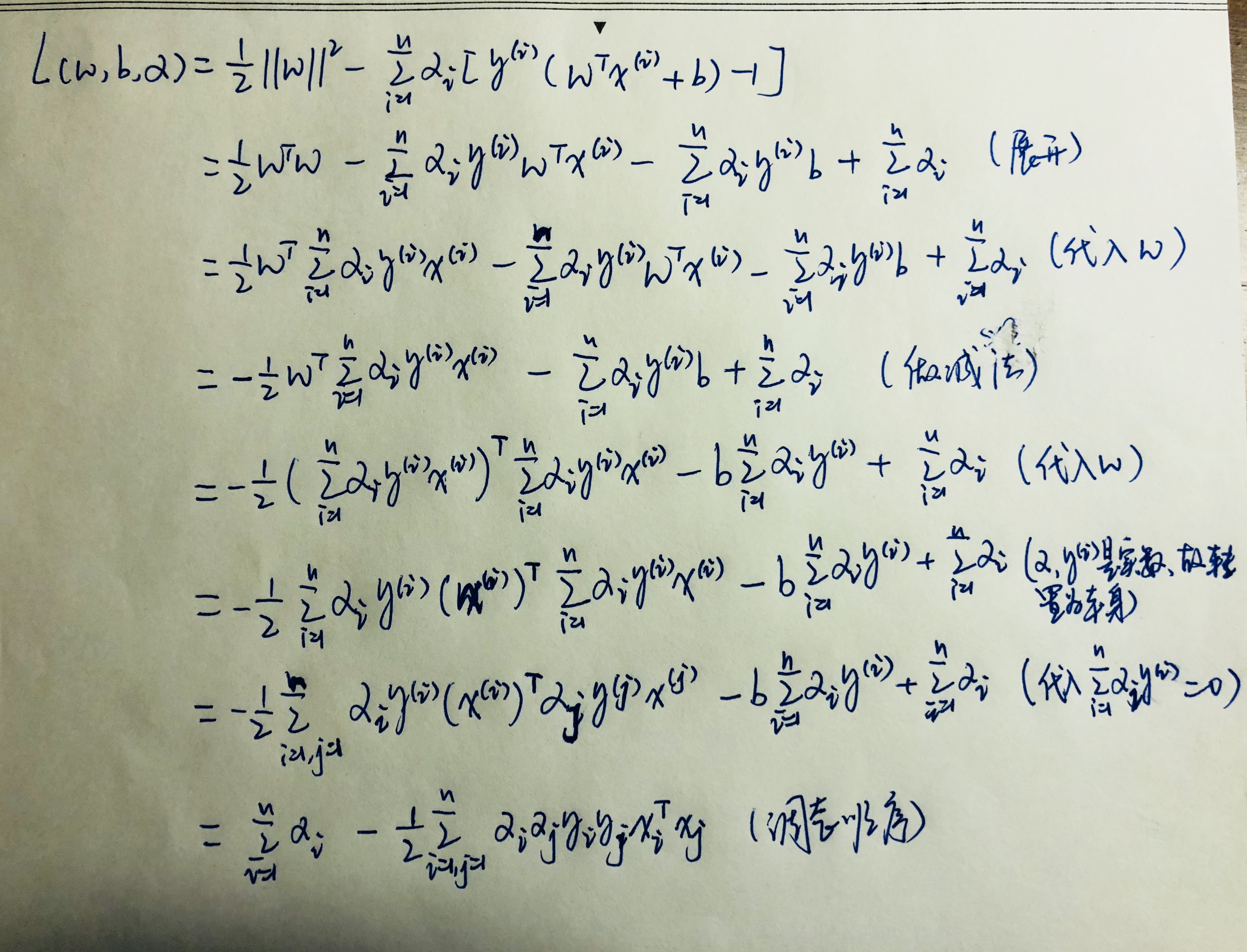
svm_lagrange_dual_1

这样求出 $\alpha$ 后即可得到 w 和 b。

svm_lagrange_dual_2

现在我们的优化问题变成了如上的形式。对于这个问题，我们有更高效的优化算法，即序列最小优化（SMO）算法。我们通过这个优化算法能得到α，再根据α，我们就可以求解出w和b，进而求得我们最初的目的：找到超平面，即”决策平面”。

SMO 算法

https://zhuanlan.zhihu.com/p/29212107
https://cloud.tencent.com/developer/article/1076970

核函数

如果数据集就是线性不可分的应该怎么处理呢？处理方法是将数据集映射到更高维的空间，变成线性可分的。如下图所示：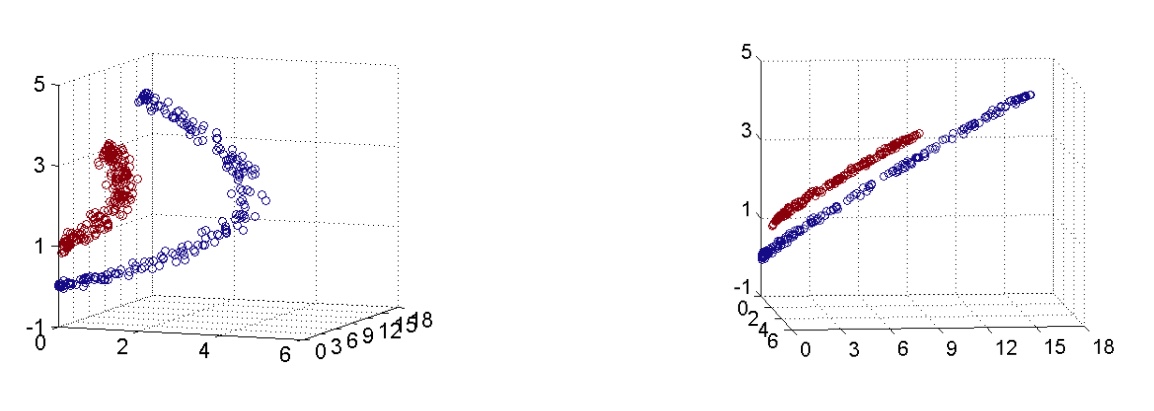
svm_kernel_demo

一般使用高斯核，但这样会导致映射后的维度非常巨大，也就是 w 的维度很大，这也是为什么要转化为对偶问题来求解的原因，对偶问题的时间复杂度只和数据集的数量有关，与维度无关。

总结 SVM

SVM 是神经网络出现之前最好的分类算法。求解 SVM 的过程也就是找到区分正负数据的最优超平面，所以引入了几何间隔的概念。而求解最大的几何间隔的问题即是在不等式约束条件下求解最优解的问题。这就引入了拉格朗日对偶问题，接着针对对偶问题求解，引入快速学习算法 SMO，最终找到超平面。
对于原始数据线性不可分的情况，引入核函数映射到高维计算，这其中 SVM 求解过程的时间复杂度与维度无关。

附一个很精髓的 SVM十问十答。

SVM 优缺点

优点：

可用于线性/非线性分类
可以解决高维问题，即大型特征空间;
泛化错误率低
结果容易解释
可以避免神经网络结构选择和局部极小点问题
SVM 尽量保持与样本间距离的性质导致它抗攻击的能力更强

缺点：

对参数调节和和函数的选择敏感，原始分类器不加修改仅适用于处理二分类问题
在大规模训练样本下，效率不高
对非线性问题有时很难找到一个合适的核函数
解决多分类问题存在困难

附录

点到平面的距离

$d$ 维空间中的超平面由下面的方程确定: $w^Tx+b=0$，其中，$w$ 与 $x$ 都是 $d$ 维列向量， $x=(x_1,x_2,…,x_d)^T$ 为平面上的点， $w=(w_1,w_2,…,w_d)^T$为平面的法向量。$b$ 是一个实数，代表平面与原点之间的距离。

Reference

http://blog.csdn.net/v_july_v/article/details/7624837
http://guoze.me/2014/11/26/svm-knowledge/
https://pdfs.semanticscholar.org/59ee/e096b49d66f39891eb88a6c84cc89acba12d.pdf
http://luojinping.com/2018/03/04/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E4%B9%98%E5%AD%90%E6%B3%95/