连续
设 $y=f(x)$ 在 $x_0$ 有定义,若
$\displaystyle\lim_{x\to x_0}{f(x)}=f(x_0)$
则函数 $f(x)$ 在点 $x_0$ 处连续。
另外一种定义:
在点 $x_0$ 附近,如果自变量的该变量是无穷小时,对应的因变量的该变量也是无穷小,则这个函数在点 $x_0$ 处连续。
通俗地说,所谓“连续”,就是不间断。放到函数上,就是没有“断点”(但是可以有“拐点”)。
二元函数的连续性定义与一元函数类似。
导数
定义
导数(Derivative)是微积分学中重要的基础概念。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。导数的本质是通过极限的概念对函数进行局部的线性逼近。
导数的几何定义是:曲线上的纵坐标对点的横坐标的导数是曲线在该点的切线的斜率。
导数的物理意义之一是:位移s对时间t的导数是瞬时速度,即 $v=\frac{ds}{dt}$
可导
函数可导定义:
(1)设 f(x)在 $x_0$ 及其附近有定义,则当 $\displaystyle\lim_{\Delta{x}\to0}{\frac{f(x_0+\Delta{x})-f(x_0)}{a}}$ 存在, 则称 f(x) 在 $x_0$ 处可导。
(2)若对于区间 (a,b) 上任意一点 (x,f(x)) 均可导,则称 f(x) 在 (a,b) 上可导。
左导数:$\displaystyle\lim_{\Delta{x}\to0^-}{\frac{f(x_0+\Delta{x})-f(x_0)}{a}}$
右导数:$\displaystyle\lim_{\Delta{x}\to0^+}{\frac{f(x_0+\Delta{x})-f(x_0)}{a}}$
连续函数可导条件:函数在该点的左右偏导数都存在且相等。
即就是一个函数在某一点求极限,如果极限存在,则为可导,若所得导数等于函数在该点的函数值,则函数为连续可导函数,否则为不连续可导函数。
微分
在数学中,微分是对函数的局部变化率的一种线性描述。微分可以近似地描述当函数自变量的取值作足够小的改变时,函数的值是怎样改变的。
定义
若 y=f(x) 在处可导,则函数的增量,
$\Delta{y}=f(x+\Delta{x})-f(x)=f’(x)\Delta{x}+\alpha(\Delta{x})\Delta{x}$
其中 $\alpha(\Delta{x})$ 是$\Delta{x}(\Delta{x} \to 0)$ 的高阶无穷小。
称 $f’(x)\Delta{x}$ 为 $f(x)$ 在 $x$ 处的微分。
而 $f’(x)$ 是 $f(x)$ 在 $x$ 处的导数。
可微
设函数$y= f(x)$,若自变量在点x的改变量Δx与函数相应的改变量Δy有关系$Δy=AΔx+ο(Δx)$
其中A与Δx无关,则称函数f(x)在点x可微,并称AΔx为函数f(x)在点x的微分,记作dy,即$dy=AΔx$
当$x=x_0$时,则记作$dy∣x=x_0$.
可微条件:
必要条件:若函数在某点可微,则该函数在该点对x和y的偏导数必存在。
充分条件:若函数对x和y的偏导数在这点的某一邻域内都存在,且均在这点连续,则该函数在这点可微。
连续但不可微的例子: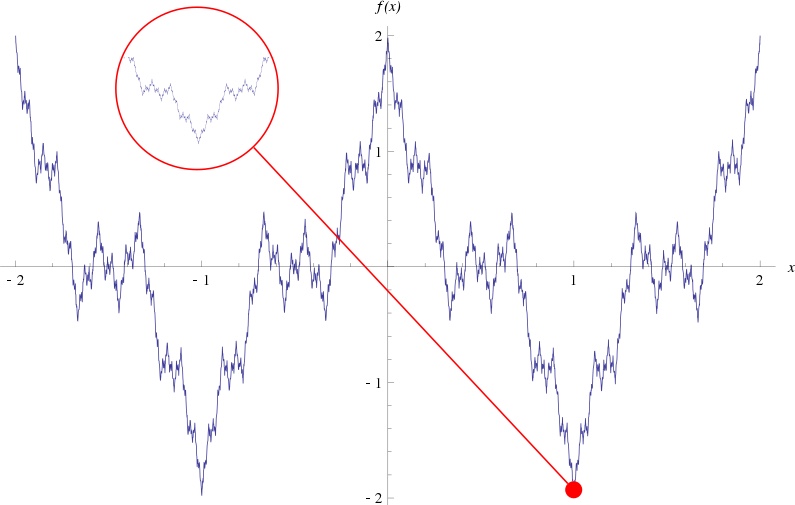
魏尔斯特拉斯函数连续,但在任一点都不可微
连续,可导,可微的关系
- 一元函数:可导必然连续,连续推不出可导,可导与可微等价。
- 多元函数:可偏导与连续之间没有联系,也就是说可偏导推不出连续,连续推不出可偏导。
- 多元函数中可微必可偏导,可微必连续,可偏导推不出可微,但若一阶偏导具有连续性则可推出可微。
全微分
对于多元函数,如果两个自变量都变化的话,这时候函数的微分就称为全微分。如果函数z=f(x,y)在(x,y)处的全增量$\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$可以写成$\Delta z=A\Delta x+B\Delta y+o(\rho)$,
取其线性主部,称为二元函数的全微分 $\Delta z=A\Delta x+B\Delta y$
可以证明全微分又可写成$dz=f_x dx+f_ydy =\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy$
上式又称为全微分的叠加原理。可以这么理解:全增量包含两个部分,$\Delta x$引起的函数值增量和$\Delta y$引起的函数值增量。
一句话感性说全微分其实就在表达曲面在某一点处的切平面。
梯度
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
例如:在一元函数 f(x) 中,梯度只能沿 x 轴正方向或负方向,而在二元函数 f(x,y) 中,梯度则是一个二维向量 (∂f/∂x,∂f/∂y)。
梯度一个重要的性质:梯度跟函数等高线是垂直的。
证明:
假设 Δx,Δy 是两个极小的变化量,根据全微分的知识,可以得到:
f(x+Δx,y+Δy)≈f(x,y)+∂f∂xΔx+∂f∂yΔy
如果 (Δx,Δy) 是在等高线方向的增量,那么 f(x+Δx,y+Δy)≈f(x,y),这意味着 ∂f∂xΔx+∂f∂yΔy=0,换句话说,向量 ∇f 和向量 (Δx,Δy) 的内积为 0。所以,梯度和函数的等高线是垂直的。
Reference
http://jermmy.xyz/2017/07/27/2017-7-27-understand-lagrange-multiplier/
