概率论在机器学习中扮演着一个核心角色,因为机器学习算法的设计通常依赖于对数据的概率假设。
随机变量在概率论中扮演着一个重要角色。最重要的一个事实是,随机变量并不是变量,它们实际上是将(样本空间中的)结果映射到真值的函数。我们通常用一个大写字母来表示随机变量。
条件分布
条件分布为概率论中用于探讨不确定性的关键工具之一。它明确了在另一随机变量已知的情况下(或者更通俗来说,当已知某事件为真时)的某一随机变量的分布。
正式地,给定$Y=b$时,$X=a$的条件概率定义为:
其中,$P(Y=b)>0$
独立性
在概率论中,独立性是指随机变量的分布不因知道其它随机变量的值而改变。在机器学习中,我们通常都会对数据做这样的假设。例如,我们会假设训练样本是从某一底层空间独立提取;并且假设样例i的标签独立于样例j(i≠j)的特性。
从数学角度来说,随机变量X独立于Y,当:
P(X)=P(X|Y)
注意,上式没有标明X,Y的取值,也就是说该公式对任意X,Y可能的取值均成立。)
利用等式(2),很容易可以证明如果X对Y独立,那么Y也独立于X。当X和Y相互独立时,记为X⊥Y。
对于随机变量X和Y的独立性,有一个等价的数学公式:
P(X,Y)=P(X)P(Y)
我们有时也会讨论条件独立,就是当我们当我们知道一个随机变量(或者更一般地,一组随机变量)的值时,那么其它随机变量之间相互独立。正式地,我们说“给定Z,X和Y条件独立”,如果:
P(X|Z)=P(X|Y,Z)
或者等价的:
P(X,Y|Z)=P(X|Z)P(Y|Z)
链式法则
我们现在给出两个与联合分布和条件分布相关的,基础但是重要的可操作定理。第一个叫做链式法则,它可以看做等式(2)对于多变量的一般形式。
定理1(链式法则):
P(X1,X2,…,Xn)=P(X1)P(X2|X1)…P(Xn|X1,X2,…,Xn−1)…………(3)
链式法则通常用于计算多个随机变量的联合概率,特别是在变量之间相互为(条件)独立时会非常有用。注意,在使用链式法则时,我们可以选择展开随机变量的顺序;选择正确的顺序通常可以让概率的计算变得更加简单。
第二个要介绍的是贝叶斯定理。利用贝叶斯定理,我们可以通过条件概率P(Y|X)计算出P(X|Y),从某种意义上说,就是“交换”条件。它也可以通过等式(2)推导出。
条件概率
条件概率
如果 A,B 是条件组 S 下的随机事件,事件 A 发生的概率随事件 B 是否发生而变化,同样,事件 B 发生的概率也随事件 A 是否发生而变化。
事件 A 在另外一个事件 B 已经发生条件下的发生概率称为条件概率,表示为P(A|B),读作「在 B 条件下 A 的概率」。
当 P(B) > 0 时,有:
P.S. 如果 A,B 是独立事件,则 A 发生的概率与 B 无关,那么 $P(A|B) = P(A)$,并且 $P(AB)=P(A)P(B)$。
联合概率
联合概率表示两个事件共同发生的概率。A 与 B 的联合概率表示为
$P(A\cap B)$ 或者 ${\displaystyle P(A,B)}$ 或者 $P(A,B)$。
边缘概率
边缘概率是某个事件发生的概率。边缘概率是这样得到的:在联合概率中,把最终结果中不需要的那些事件合并成其事件的全概率而消失(对离散随机变量用求和得全概率,对连续随机变量用积分得全概率)。这称为边缘化(marginalization)。A的边缘概率表示为$P(A)$,B的边缘概率表示为$P(B)$。
全概率公式
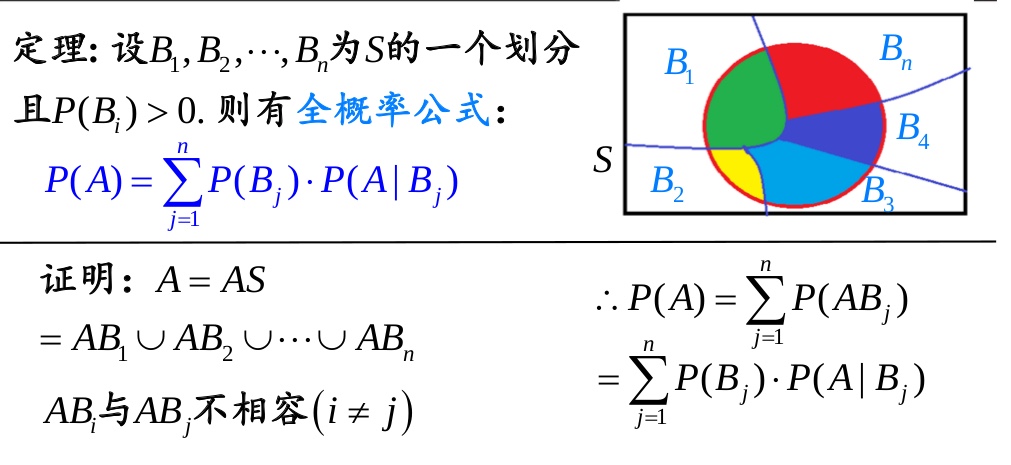
贝叶斯定理
https://zh.wikipedia.org/wiki/%E6%9D%A1%E4%BB%B6%E6%A6%82%E7%8E%87
http://blog.csdn.net/u012566895/article/details/51220127
http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html
