生成学习算法介绍
有监督机器学习可以分为判别学习算法(generative learning algorithm)和生成学习算法(discriminative learning algorithm)。
- 判别学习算法常见的有:逻辑回顾,支持向量机等。
- 生成学习算法常见的有:混合高斯模型、朴素贝叶斯法和隐形马尔科夫模型等。
判别学习算法是直接学习 p(y|x) 或者是从输入直接映射到输出的算法。
生成学习算法是计算变量x在变量y上的条件分布p(x|y)和变量y的分布p(y) ,然后使用贝叶斯公式: $p(y|x)=\frac{p(x,y)}{p(x)}=\frac{p(y)*p(x|y)}{p(x)}$ 计算出p(y|x)。
针对课程中提到的两种生成学习算法中,高斯判别分析(Gaussian Discriminant Analysis)和朴素贝叶斯(Navie Bayes)分别解决了两种场景下的问题。
GDA 是针对的是特征向量 X 为连续值时的问题,而 Navie Bayes 则针对的是特征向量为离散值时的问题。
高斯判别分析
多维正态分布(The multivariate normal distribution)
假设随机变量 $X$ 满足 $n$ 维的多项正态分布,参数为均值向量 $μ ∈ R^{n} $,协方差矩阵$Σ ∈ R^{n×n}$,记为 $N(μ,Σ)$ 其概率密度表示为:
$detΣ$ 表示矩阵 $Σ$ 的行列式(determinant)。
均值向量: $μ$
协方差矩阵: $Σ=E[(X−E[X])(X−E[X])T]=E[(x−μ)(x−μ)T]$
高斯判别分析
GDA 模型针对的是输入特征为连续值时的分类问题,这个模型的基本假设是目标值 y 服从伯努利分布(0-1分布),条件概率 P(x|y) 服从多元正态分布((multivariate normal distribution)),即:
$y∼Bernoulli(\phi)$
$P(x|y=0)∼N(μ_0,\Sigma)$
$P(x|y=1)∼N(μ_1,\Sigma)$
它们的概率密度为:
我们模型的参数包括,$\phi,\Sigma,μ_0,μ_1$ 注意到,我们使用了两种不同的均值向量$μ_0$和$μ_1$,但是使用了同一种协方差矩阵 $\Sigma$, 则我们的极大似然函数的对数如下所示:
对极大似然函数对数最大化,我们就得到了GDA模型各参数的极大虽然估计(略)。
GDA 与 LR
前面我们提到:
我们有:
上式实际上可以表示成logistic函数的形式:
其中,θ是参数ϕ,μ0,μ1,Σθ是参数ϕ,μ0,μ1,Σ某种形式的函数。GDA的后验分布可以表示logistic函数的形式。
下图为用 GDA 对两类样本分别拟合高斯概率密度函数p(x|y=0)和p(x|y=1),得到两个钟形曲线。沿x轴遍历样本,在x轴上方画出相应的p(y=1|x)。如选x轴靠左的点,那么它属于1的概率几乎为0,p(y=1|x)=0,两条钟形曲线交点处,属于0或1的概率相同,p(y=1|x)=0.5,x轴靠右的点,输出1的概率几乎为1,p(y=1|x)=1。最终发现,得到的曲线和sigmoid函数曲线很相似。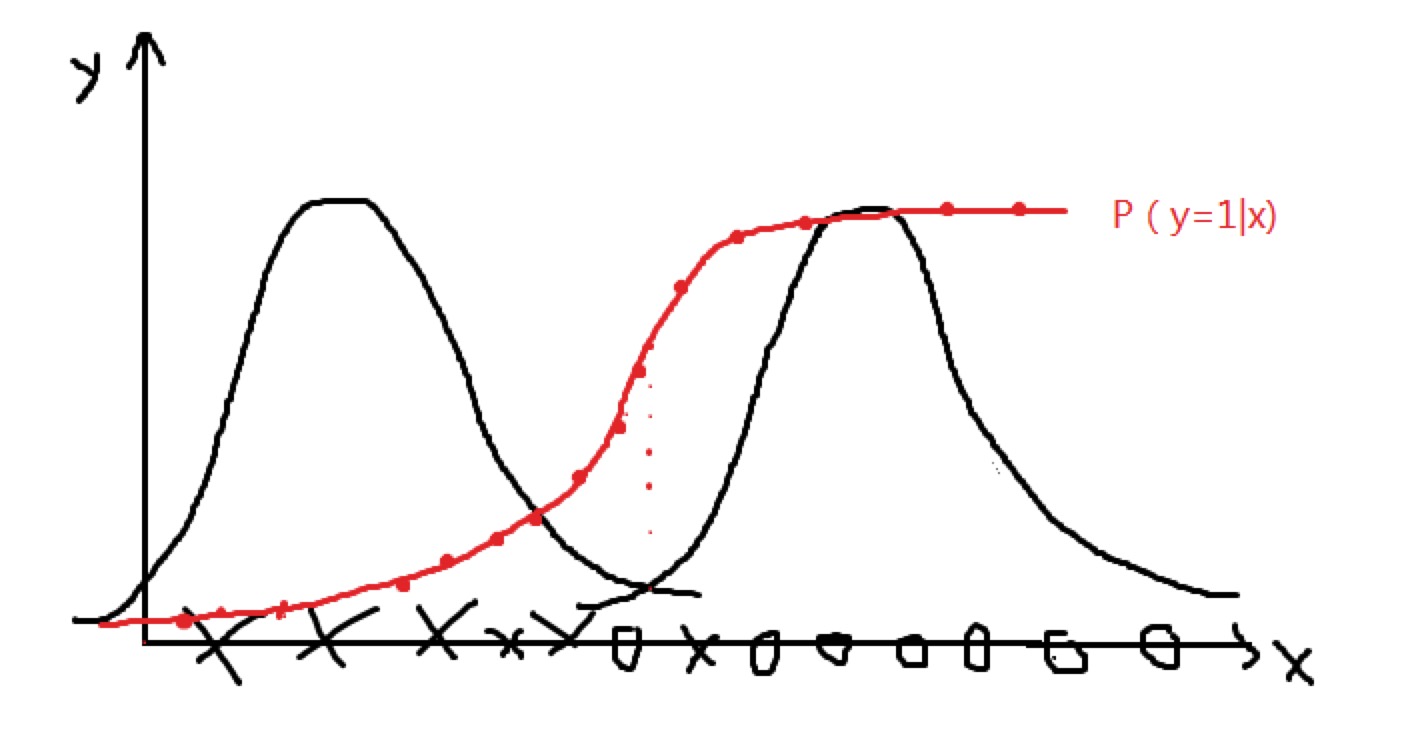
实际上,可以证明,不仅仅当先验概率分布服从多变量正态分布时可以推导出逻辑回归的模型,当先验分布属于指数分布簇中的任何一个分布,如泊松分布时,都可以推导出逻辑回归模型。而反之不成立,逻辑回归的先验概率分布不一定必须得是指数分布簇中的成员。基于这些原因,在实践中使用逻辑回归比使用GDA更普遍。
生成学习算法比判决学习算法需要更少的数据。如GDA的假设较强,所以用较少的数据能拟合出不错的模型。而逻辑回归的假设较弱,对模型的假设更为健壮,拟合数据需要更多的样本。
朴素贝叶斯
考虑自变量比较多的情况,比如垃圾邮件的识别需要检测成百上千甚至上万的字符是否出现,如有免费、购买等类似的词出现的邮件很大可能是垃圾邮件。这种情况下若有k个自变量,考虑各变量之间的交互作用就需要计算$2^k$次,为了简化计算量对模型作一个更强的假设:
给定因变量 y 的值,各自变量之间相互独立.
所以有
第一个等式是根据通常的概率论得到的,第二个等式是根据贝叶斯假设得到的。虽然贝叶斯假设是个很强的假设,但是实践证明在许多问题上都表现得很好。
参数的极大似然估计及p(y|x)的推导过程略。
拉普拉斯平滑
拉普拉斯平滑(Laplace Smoothing)又称为加1平滑。平滑方法的存在是为了解决零概率问题。
所谓的零概率问题,就是在计算新实例的概率时,如果某个分量在训练集中从没出现过,会导致整个实例的概率计算结果为0,针对文本分类问题就是当一个词语在训练集中没有出现过,那么该词语的概率为0,使用连乘计算文本出现的概率时,整个文本出现的概率也为0,这显然不合理,因为不能因为一个事件没有观测到就判断该事件的概率为0.
Reference
http://xtf615.com/2017/03/25/%E7%94%9F%E6%88%90%E7%AE%97%E6%B3%95/
http://blog.csdn.net/v1_vivian/article/details/52190572
http://www.cnblogs.com/mikewolf2002/p/7763475.html
